题目内容
如图，四边形ABCD是一个边长为1的正方形，△MPN是正方形的一个内接正三角形，且MN∥AB，若向正方形内部随机投入一个质点，则质点恰好落在△MPN的概率为（ ）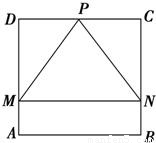
A．
B．
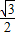
C．
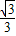
D．
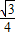
【答案】分析：先明确是几何概型中的面积类型，设正方形的边长为1，求得其面积，再求其内接三角形的面积，由概率公式求得要应面积的比值即可．
解答：解：根据题意是几何概型
设正方形的边长为1，其面积为1
因为三角形为其内接三角形，且MN∥AB
所以三角形的边长为1，其高为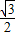
所以三角形的面积为：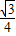
质点落在三角形MNP内的概率P=
=
=
．
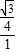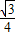故选D
点评：本题主要考查几何概型中的面积类型，方法是分别求相应面积，再求其比值．
解答：解：根据题意是几何概型
设正方形的边长为1，其面积为1
因为三角形为其内接三角形，且MN∥AB
所以三角形的边长为1，其高为
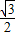
所以三角形的面积为：
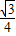
质点落在三角形MNP内的概率P=
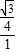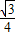==．故选D
点评：本题主要考查几何概型中的面积类型，方法是分别求相应面积，再求其比值．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
如图，四边形ABCD与A′ABB′都是边长为a的正方形，点E是A′A的中点，A′A⊥平面ABCD．
如图，四边形ABCD为正方形，QA⊥平面ABCD，PD∥QA，QA=AB=
如图，四边形ABCD为矩形，且AD=2，AB=1，PA⊥平面ABCD，PA=1，E为BC的中点．
如图，四边形ABCD内接于⊙O，如果它的一个外角∠DCE=64°，那么∠BOD
如图，四边形ABCD为正方形，PD⊥平面ABCD，PD∥QA，QA=AB=