Question

函数f(x)=log

1

2

(sinx-cosx)的定义域是

 

，值域是

 

．

Answer 1

分析：根据题意，对数函数的定义域要求对数的真数大于0，利用三角函数的图象，求出定义域，先利用两角和公式对sinx-cosx化简整理，进而根据正弦函数的性质求得函数的最大和最小值，即可求出值域．

解答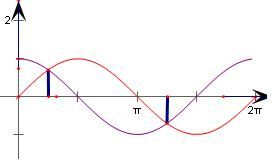：解：sinx-cosx＞0
即sinx＞cosx
结合图象
可知在一个周期[0，2π]上，
满足条件的范围是（

π

4

，

5π

4

）
∴函数的定义域{x|2kπ+

π

4

＜x＜2kπ+

5π

4

，k∈Z}．
y=sinx-cosx=

2

sin（x-

π

4

）
∵sinx-cosx＞0
∴0＜

2

sin（x-

π

4

）≤

2

∴函数的值域为{y|y≥-

1

2

}
故答案为：{x|2kπ+

π

4

＜x＜2kπ+

5π

4

，k∈Z}，{y|y≥-

1

2

}

点评：本题主要考查了对数函数的定义域和值域．解题的关键是对sinx-cosx的化简，以及对正弦函数的基础知识的熟练记忆．