题目内容
简答题
解不等式|![]() |+|log3(3-x)|≥1.
|+|log3(3-x)|≥1.
答案:
解析:
解析:
|
解:要使原不等式有意义,则 令 (1)当0<x≤1时,原不等式可化为-log3x+log3(3-x)≥1. ∴log3(3-x)≥1+log3x=log3(3x), ∴3-x≥3x,∴x≤ (2)当1<x<2时,原不等式可化为log3x+log3(3-x)≥1. 即log3[x(3-x)]≥1,∴x(3-x)≥3. 即x2-3x+3≤0.此不等式无解. (3)当2≤x<3时,原不等式可化为log3x-log3(3-x)≥1,即log3x≥1+log3(3-x) ∴log3x≥log3[3(3-x)],∴x≥3(3-x),∴x≥ 故 综上可得,原不等式的解集为{x|0<x≤ |

练习册系列答案
相关题目
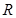 上的奇函数
上的奇函数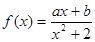 (
(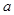 、
、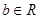 )过已知点
)过已知点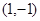 .
.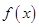 在区间
在区间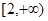 是增函数;若函数
是增函数;若函数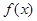 在区间
在区间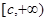 (其中
(其中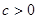 )也是增函数,求
)也是增函数,求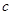 的最小值;
的最小值;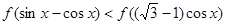 的解集.
的解集.