题目内容
下列表示的关系中:①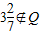 ;②{2}∈{x|x≥2};③-10∈{x|x=3k-1,k∈Z};④
;②{2}∈{x|x≥2};③-10∈{x|x=3k-1,k∈Z};④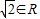 ;⑤∅?{x|x2-1=0},其中错误的个数为( )
;⑤∅?{x|x2-1=0},其中错误的个数为( )A.1个
B.2个
C.3个
D.4个
【答案】分析:根据集合的含义与表示,对5个选项分别加以论证,可得①、②是假命题,而③、④、⑤是真命题,由此不难得到本题的答案.
解答:解:对于①,因为 是有理数,得“
是有理数,得“ ”是假命题,所以①不正确;
”是假命题,所以①不正确;
对于②,集合{2}?{x|x≥2},而不是{2}∈{x|x≥2},符号用错,故②不正确;
对于③,当k=-3时,x=3k-1=-10,故-10∈{x|x=3k-1,k∈Z}是真命题,得③正确;
对于④,因为 是实数,故“
是实数,故“ ”是真命题,得④正确;
”是真命题,得④正确;
对于⑤,因为{x|x2-1=0}={-1,1}有两个元素,故∅?{x|x2-1=0},得⑤正确.
综上所述,错误的命题是①、②,共2个
故选:B
点评:本题给出关于集合的几个命题,叫我们判断它们的真假,着重考查了命题的真假判断与应用、集合有关概念等知识,属于基础题.
解答:解:对于①,因为
 是有理数,得“
是有理数,得“ ”是假命题,所以①不正确;
”是假命题,所以①不正确;对于②,集合{2}?{x|x≥2},而不是{2}∈{x|x≥2},符号用错,故②不正确;
对于③,当k=-3时,x=3k-1=-10,故-10∈{x|x=3k-1,k∈Z}是真命题,得③正确;
对于④,因为
 是实数,故“
是实数,故“ ”是真命题,得④正确;
”是真命题,得④正确;对于⑤,因为{x|x2-1=0}={-1,1}有两个元素,故∅?{x|x2-1=0},得⑤正确.
综上所述,错误的命题是①、②,共2个
故选:B
点评:本题给出关于集合的几个命题,叫我们判断它们的真假,着重考查了命题的真假判断与应用、集合有关概念等知识,属于基础题.

练习册系列答案
相关题目
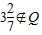 ;②{2}∈{x|x≥2};③-10∈{x|x=3k-1,k∈Z};④
;②{2}∈{x|x≥2};③-10∈{x|x=3k-1,k∈Z};④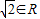 ;⑤∅?{x|x2-1=0},其中错误的个数为( )
;⑤∅?{x|x2-1=0},其中错误的个数为( )