题目内容
已知函数f（x）=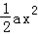
﹣（2a+1）x+2lnx（a∈R）．
（Ⅰ）求 f（x）的单调区间；
（Ⅱ）设 g（x）= x2﹣2x，若对任意 x1 ∈（0，2]，均存在x2∈（0，2]，使得 f（x1）＜ g（x2 ），求a的取值范围．
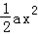﹣（2a+1）x+2lnx（a∈R）．（Ⅰ）求 f（x）的单调区间；
（Ⅱ）设 g（x）= x2﹣2x，若对任意 x1 ∈（0，2]，均存在x2∈（0，2]，使得 f（x1）＜ g（x2 ），求a的取值范围．
解：（Ⅰ）函数的定义域为（0，+∞），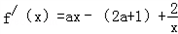
=
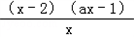
当a=0时，单调减区间为（0，2），单调增区间为（2，+∞）；
当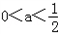
时，单调减区间为（2，
），单调增区间为（﹣∞，2），（
；
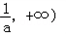当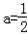
时，单调增区间为（0，+∞）；
当a＜0或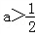
时，单调减区间为（﹣∞，
），（2，+∞）；单调增区间为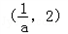
；
（Ⅱ） 由已知，转化为f（x）max＜g（x）max．由x∈（0，2]，得到g（x）max=g（2）=0，
由（Ⅰ）知当a=0时，不成立；
当a＞0时，f（x）max =f（2）=﹣2a﹣2+2ln2，
所以 a＞﹣1+ln2
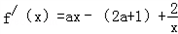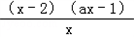
=当a=0时，单调减区间为（0，2），单调增区间为（2，+∞）；
当
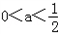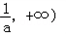时，单调减区间为（2，），单调增区间为（﹣∞，2），（；当
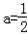时，单调增区间为（0，+∞）；当a＜0或
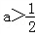时，单调减区间为（﹣∞，），（2，+∞）；单调增区间为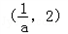；（Ⅱ） 由已知，转化为f（x）max＜g（x）max．由x∈（0，2]，得到g（x）max=g（2）=0，
由（Ⅰ）知当a=0时，不成立；
当a＞0时，f（x）max =f（2）=﹣2a﹣2+2ln2，
所以 a＞﹣1+ln2
练习册系列答案
相关题目
已知函数f（x）=x2-bx的图象在点A（1，f（1））处的切线l与直线3x-y+2=0平行，若数列{
}的前n项和为Sn，则S2010的值为（ ）
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|