题目内容
(本题满分12分)设平面直角坐标系 中,设二次函数
中,设二次函数 的图象与两坐标轴有三个交点,经过这三个交点的圆记为C.求:
的图象与两坐标轴有三个交点,经过这三个交点的圆记为C.求:
(1)求实数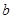 的取值范围;
的取值范围;
(2)求圆C 的方程;
(3)问圆C 是否经过某定点(其坐标与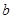 无关)?请证明你的结论.
无关)?请证明你的结论.
 中,设二次函数
中,设二次函数 的图象与两坐标轴有三个交点,经过这三个交点的圆记为C.求:
的图象与两坐标轴有三个交点,经过这三个交点的圆记为C.求:(1)求实数
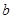 的取值范围;
的取值范围;(2)求圆C 的方程;
(3)问圆C 是否经过某定点(其坐标与
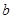 无关)?请证明你的结论.
无关)?请证明你的结论.(1)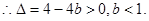
(2)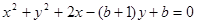
(3)圆恒过点(0,1)
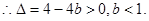
(2)
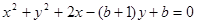
(3)圆恒过点(0,1)
试题分析:解:(1)由题意可知,方程
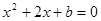 有两不等3根,
有两不等3根,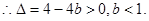
(2)设圆C 的方程为:
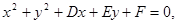
圆C与
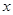 轴的交点和二次函数
轴的交点和二次函数 的图象与
的图象与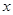 轴的交点相同,
轴的交点相同,所以在圆的方程
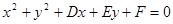 中令
中令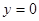 ,得
,得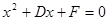 应为
应为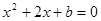 ,所以
,所以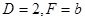 ;
;因为圆C过点
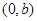 ,在圆的方程
,在圆的方程 中令
中令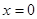 ,得
,得方程
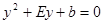 有根
有根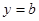 ,代入得:
,代入得: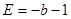 ,
,所求圆C的方程为:
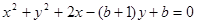
(3)圆C的方程可改写为:
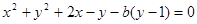 ,所以圆恒过点(0,1)。
,所以圆恒过点(0,1)。点评:解决该试题的关键是利用一般是待定系数法求解圆的方程,属于基础题。

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
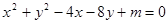 与
与 轴相切。
轴相切。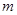 的值;
的值;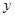 轴上截得的弦长;
轴上截得的弦长; 是直线
是直线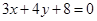 上的动点,过点
上的动点,过点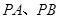 与圆M相切,
与圆M相切,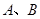 为切点。求四边形
为切点。求四边形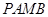 面积的最小值。
面积的最小值。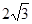 ,连接OC,CD⊥OC交⊙O于D,则CD的最大值为_____________.
,连接OC,CD⊥OC交⊙O于D,则CD的最大值为_____________.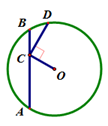
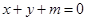 与圆
与圆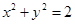 交于不同的两点A、B,O是坐标原点,且
交于不同的两点A、B,O是坐标原点,且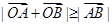 ,则实数m的取值范围是 。
,则实数m的取值范围是 。 上的点到直线
上的点到直线 距离的最大值是( )
距离的最大值是( ) 
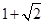


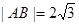 ,求a的值;
,求a的值;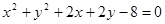 与圆C2:
与圆C2: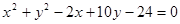 相交于A、B两点。
相交于A、B两点。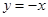 上,且过A、B两点的圆的方程;
上,且过A、B两点的圆的方程;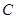 与定圆
与定圆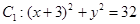 内切,与定圆
内切,与定圆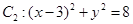 外切,A点坐标为
外切,A点坐标为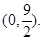 (1)求动圆
(1)求动圆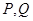 满足
满足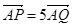 ,求
,求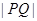 的值.
的值. 过定点
过定点 ,且与直线
,且与直线 相切,椭圆
相切,椭圆 的对称轴为坐标轴,一个焦点为
的对称轴为坐标轴,一个焦点为 ,点
,点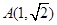 在椭圆
在椭圆 的方程及椭圆
的方程及椭圆 与轨迹
与轨迹 处的切线平行,且直线
处的切线平行,且直线 两点,试求当
两点,试求当 面积取到最大值时直线
面积取到最大值时直线