Question

(本小题满分12分)

已知以原点为中心,F(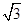,0)为右焦点的椭圆C,过点F垂直于轴的弦AB长为4.

(1).求椭圆C的标准方程.

(2).设M、N为椭圆C上的两动点，且，点P为椭圆C的右准线与轴的交点，求的取值范围.

 

Answer 1

【答案】

 

解：（1）.设椭圆C的标准方程.为,则

   即

椭圆C的标准方程为

(2).设直线MN方程为,,则

得

,

由得,即

,

,此时,椭圆C的右准线方程为,则P(,0)

===

由,令， 则=     

=    当时 =0

当时,0<

当时,0>

当轴时，设M、N则

===

故的取值范围是

【解析】略