题目内容
.(本小题满分12分)
如图4所示的茎叶图记录了甲、乙两个小组(每小组4人)在期末考试中
的数学成绩.乙组记录中有一个数据模糊,无法确认,在图中以 表示.
表示.
已知甲、乙两个小组的数学成绩的平均分相同.
(1)求 的值;
的值;
(2)求乙组四名同学数学成绩的方差;
(3)分别从甲、乙两组同学中各随机选取一名同学,记这两名同学数学
成绩之差的绝对值为 ,求随机变量
,求随机变量 的分布列和均值(数学期望).
的分布列和均值(数学期望).
如图4所示的茎叶图记录了甲、乙两个小组(每小组4人)在期末考试中
的数学成绩.乙组记录中有一个数据模糊,无法确认,在图中以
 表示.
表示.已知甲、乙两个小组的数学成绩的平均分相同.
(1)求
 的值;
的值;(2)求乙组四名同学数学成绩的方差;
(3)分别从甲、乙两组同学中各随机选取一名同学,记这两名同学数学
成绩之差的绝对值为
 ,求随机变量
,求随机变量 的分布列和均值(数学期望).
的分布列和均值(数学期望).
(1) 依题意,得
 , 解得
, 解得 .
. (2) 根据已知条件,可以求得两组同学数学成绩的平均分都为
 .
. 所以乙组四名同学数学成绩的方差为
 .
.(3) 分别从甲、乙两组同学中各随机选取一名同学,共有
 种可能的结果.
种可能的结果.  这两名同学成绩之差的绝对值
这两名同学成绩之差的绝对值 的所有情况如下表:
的所有情况如下表:| | 87 | 89 | 96 | 96 |
| 87 | 0 | 2 | 9 | 9 |
| 93 | 6 | 4 | 3 | 3 |
| 93 | 6 | 4 | 3 | 3 |
| 95 | 8 | 6 | 1 | 1 |
 的所有可能取值为
的所有可能取值为 .
.由表可得
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, .
.所以随机变量
 的分布列为:
的分布列为: | 0 | 1 | 2 | 3 | 4 | 6 | 8 | 9 |
 |  |  |  |  |  |  |  |  |
 的数学期望为
的数学期望为

 .
. 略

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目

 岁的人群随机抽取
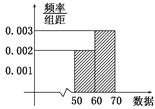
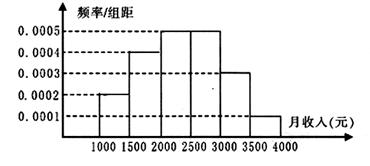
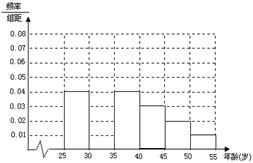
岁的人群随机抽取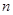 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图: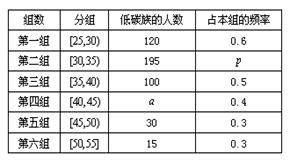
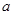 、
、 的值;
的值;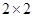 维列表,并判断能否有99.9%的把握认定该地区的生活习惯是否符合低碳观念与人的年龄有关?
维列表,并判断能否有99.9%的把握认定该地区的生活习惯是否符合低碳观念与人的年龄有关?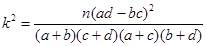
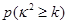
 年龄组
年龄组
 的样本,样本中A型号产品有15件,那么样本容量
的样本,样本中A型号产品有15件,那么样本容量 必过( )
必过( ) B.点
B.点 C.点
C.点 D.点
D.点