题目内容
在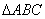 中,
中,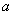 ,
,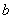 ,
,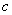 分别是角
分别是角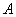 ,
,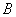 ,
,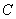 的对边,
的对边,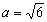 ,
,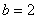 ,且
,且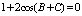 ,则
,则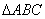 的
的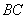 边上的高等于( )
边上的高等于( )
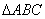 中,
中,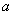 ,
,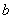 ,
,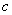 分别是角
分别是角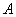 ,
,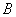 ,
,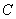 的对边,
的对边,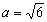 ,
,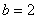 ,且
,且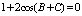 ,则
,则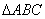 的
的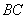 边上的高等于( )
边上的高等于( )A. | B. | C. | D. |
C
试题分析:△ABC中,由1+2cos(B+C)=0可得
 (B+C)=
(B+C)= ,∴B+C=120°,∴A=60°.
,∴B+C=120°,∴A=60°.由余弦定理可得
 ,解得
,解得 .
.由△ABC的面积等于
 ,(h为BC边上的高)可得
,(h为BC边上的高)可得 .
. 。
。点评:本题主要考查余弦定理的应用,三角形的内角和公式,考查三角形面积的计算,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的值为( )
的值为( )




 ,试判断△ABC的形状;
,试判断△ABC的形状; ,b+c=3,求b和c的值.
,b+c=3,求b和c的值. ----------①
----------① ------②
------② ------③
------③ 有
有
 .
. 的值。
的值。 ;
; ,则
,则 的值为( )
的值为( )



 的值
的值 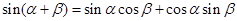 ------①
------① ------②
------② ------③
------③ 有
有
 .
.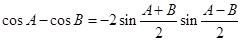 ;
; 的三个内角
的三个内角 满足
满足 ,试判断
,试判断 ,则
,则 ___________.
___________.