题目内容
已知函数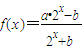 是定义在R上的奇函数,其反函数的图象过点
是定义在R上的奇函数,其反函数的图象过点 ,若x∈(-1,1)时,不等式
,若x∈(-1,1)时,不等式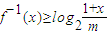 恒成立,则实数m的取值范围为 .
恒成立,则实数m的取值范围为 .
【答案】分析:根据f(x)是奇函数,则f(0)=0,结合反函数图象经过的点的坐标,列出关于a,b的方程组,可求出a,b的值,从而求出f(x)的解析式,再将x用y表示,最后交换x、y,即可求出反函数的解析式,从而得 对x∈(-1,1)恒成立根据函数在(0,+∞)上的单调性建立不等式,将m分离出来,即m≥1-x对x∈(-1,1)恒成立,从而求出所求.
对x∈(-1,1)恒成立根据函数在(0,+∞)上的单调性建立不等式,将m分离出来,即m≥1-x对x∈(-1,1)恒成立,从而求出所求.
解答:解:∵f(x)是奇函数,∴ ,
,
∴a=b①…(2分)
又其反函数的图象过点 ,得原函数过点(1,
,得原函数过点(1, ),
),
∴ ②.
②.
由①②得a=b=1.
记 .整理得
.整理得 ,
,
∴
上式两边取2为底的对数, ,交换x、y,
,交换x、y,
故所求反函数 …(8分)
…(8分)
从而 对x∈(-1,1)恒成立
对x∈(-1,1)恒成立
∵y=log2x是(0,+∞)上是增函数,
∴ …(11分)
…(11分)
即m≥1-x对x∈(-1,1)恒成立
故m的取值范围是m≥2…(13分)
故答案为:m≥2.
点评:本题主要考查了反函数,以及反函数与原函数的之间的关系,同时考查了恒成立问题和最值问题,是一道综合题.
 对x∈(-1,1)恒成立根据函数在(0,+∞)上的单调性建立不等式,将m分离出来,即m≥1-x对x∈(-1,1)恒成立,从而求出所求.
对x∈(-1,1)恒成立根据函数在(0,+∞)上的单调性建立不等式,将m分离出来,即m≥1-x对x∈(-1,1)恒成立,从而求出所求.解答:解:∵f(x)是奇函数,∴
 ,
,∴a=b①…(2分)
又其反函数的图象过点
 ,得原函数过点(1,
,得原函数过点(1, ),
),∴
 ②.
②.由①②得a=b=1.
记
 .整理得
.整理得 ,
,∴

上式两边取2为底的对数,
 ,交换x、y,
,交换x、y,
故所求反函数
 …(8分)
…(8分)从而
 对x∈(-1,1)恒成立
对x∈(-1,1)恒成立∵y=log2x是(0,+∞)上是增函数,
∴
 …(11分)
…(11分)即m≥1-x对x∈(-1,1)恒成立
故m的取值范围是m≥2…(13分)
故答案为:m≥2.
点评:本题主要考查了反函数,以及反函数与原函数的之间的关系,同时考查了恒成立问题和最值问题,是一道综合题.

练习册系列答案
相关题目

 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当 时不等式
时不等式 成立, 若
成立, 若 ,
,
 ,则
,则 的大小关系是 .
的大小关系是 . 是定义在R上的增函数,且
是定义在R上的增函数,且 ,则m的取值范围是
.
,则m的取值范围是
. 是定义在R上的奇函数,
是定义在R上的奇函数, ,
,
 ,
,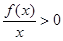 的解集是
.
的解集是
.