题目内容
已知函数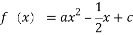 (
(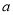 、
、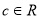 ),满足
),满足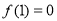 ,且
,且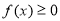 在
在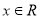 时恒成立.
时恒成立.
(1)求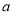 、
、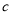 的值;
的值;
(2)若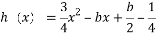 ,解不等式
,解不等式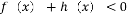 ;
;
(3)是否存在实数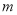 ,使函数
,使函数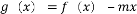 在区间
在区间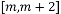 上有最小值
上有最小值 ?若存在,请求出
?若存在,请求出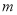 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(1) ;(2)
;(2) ,
, 或
或 .
.
【解析】
试题分析:(1)由题根据f(1)=0可以得到 ,根据
,根据 在
在 时恒成立得到
时恒成立得到 ,然后解出a,c;(2) 由
,然后解出a,c;(2) 由 得到
得到 ,然后分当
,然后分当 ,
, ,
, 讨论求得解集;(3)根据对称轴在所给区间左侧,当
讨论求得解集;(3)根据对称轴在所给区间左侧,当 ,中间,当
,中间,当 ,右侧, 当
,右侧, 当 结合所给函数满足的条件进行分类讨论求得结果.
结合所给函数满足的条件进行分类讨论求得结果.
试题解析:(1)由 ,得
,得 ,
,
因为 在
在 时恒成立,所以
时恒成立,所以 且△
且△ ,
, ,
,
即 ,
, ,
, ,所以
,所以 .
.
(2)由(1)得 ,由
,由 ,得
,得
 ,即
,即 ,
,
所以,当 时,原不等式解集为
时,原不等式解集为 ;
;
当 时,原不等式解集为
时,原不等式解集为 ;
;
当 时,原不等式解集为空集 .
时,原不等式解集为空集 .
(3) ,
,
 的图像是开口向上的抛物线,对称轴为直线
的图像是开口向上的抛物线,对称轴为直线 .
.
假设存在实数 ,使函数
,使函数 在区间
在区间 上有最小值
上有最小值 .
.
当 ,即
,即 时,函数
时,函数 在区间
在区间 上是增函数,所以
上是增函数,所以 ,即
,即 ,解得
,解得 或
或 ,
,
因为 ,所以
,所以 ;
;
②当 ,即
,即 时,函数
时,函数 的最小值为
的最小值为 ,即
,即
 ,解得
,解得 或
或 ,均舍去;
,均舍去;
③当 ,即
,即 时,
时, 在区间
在区间 上是减函数,所以
上是减函数,所以 ,即
,即 ,解得
,解得 或
或 ,因
,因 ,所以
,所以 .
.
综上,存在实数 ,
, 或
或 时,函数
时,函数 在区间
在区间 上有最小值
上有最小值 .
.
考点:恒成立问题,一元二次不等式求解,一元二次函数的性质.

练习册系列答案
相关题目
 是不等式
是不等式 成立的一个充分不必要条件,则实数
成立的一个充分不必要条件,则实数 的取值范围是( )
的取值范围是( )



 ,则
,则 的值为( )
的值为( )
 的前
的前 项和
项和 ,则其通项公式为
,则其通项公式为  是△ABC所在平面内的一点,且满足
是△ABC所在平面内的一点,且满足 ,则△ABC的形状一定是( )
,则△ABC的形状一定是( ) 是以
是以 为公差的等差数列,
为公差的等差数列, 是其前
是其前 项和,若
项和,若 是数列
是数列 中的唯一最大项,则数列
中的唯一最大项,则数列 的取值范围是______________.
的取值范围是______________. ,
, 满足约束条件
满足约束条件 ,则目标函数
,则目标函数 的取值范围为( )
的取值范围为( ) B.
B. C.
C. D.
D.
 }满足:a
}满足:a =1,a
=1,a =2a
=2a (n
(n N
N ),则a
),则a =( )
=( )