Question

已知椭圆C：

x2

a2

+

y2

b2

=1(a＞b＞0)，离心率e=

2

2

，O为坐标原点，A（a，0），B（0，b），点O到直线AB的距离为

6

3

（1）求椭圆C的方程；
（2）过M（0，2）作倾斜角为锐角的直线l交椭圆C于不同的两点P，Q，若

MP

=

2

3

MQ

，求直线l的方程．

Answer 1

分析：（1）由A（a，0），B（0，b），知直线AB的方程为bx+ay-ab=0，由点O到直线AB的距离为

6

3

，知

ab

a2+b2

=

6

3

，再由

c

a

=

2

2

，能求出椭圆方程．
（2）设直线l的斜率为k，则直线l的方程为y=kx+2，由

y=kx+2 x2 2 +y2=1

，得（2k²+1）x²+8kx+6=0，设P（x₁，y₁），Q（x₂，y₂），x1x2=

6

2k2+1

，x1+x2=

-8k

2k2+1

，由M（0，2），

MP

=

2

3

MQ

，知

MP

=（x₁，y₁-2），

MQ

=(x2，y2-2)，x1=

2

3

x2，由此能求出直线l的方程．

解答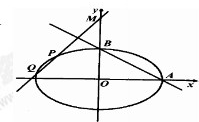：解：（1）∵A（a，0），B（0，b），
∴直线AB的方程为

x

a

+

y

b

=1，即bx+ay-ab=0，
∵点O到直线AB的距离为

6

3

，∴

ab

a2+b2

=

6

3

，①
∵离心率e=

2

2

，∴

c

a

=

2

2

②
联立①②得：a²=2，b²=1，
∴所求椭圆方程为：

x2

2

+y2=1．
（2）设P（x₁，y₁），Q（x₂，y₂），
∵M（0，2），

MP

=

2

3

MQ

，
∴

MP

=（x₁，y₁-2），

MQ

=(x2，y2-2)，
设直线l的斜率为k，则直线l的方程为y=kx+2，
由

y=kx+2 x2 2 +y2=1

，得（2k²+1）x²+8kx+6=0，
∵直线l交椭圆C于不同的两点P，Q，
∴△=（8k）²-24（2k²+1）＞0，解得k2＞

3

2

．
x1x2=

6

2k2+1

，x1+x2=

-8k

2k2+1

，
∵

MP

=

2

3

MQ

，

MP

=（x₁，y₁-2），

MQ

=(x2，y2-2)，
∴x1=

2

3

x2，

(x1+x2)2

x1x2

=

32k2

3(2k2+1)

=

25

6

，解得k2=

25

14

，
∴直线l的倾斜角为锐角，∴k=

5 14

14

，
∴直线l的方程为y=

5 14

14

x+2．

点评：本题考查椭圆方程的求法，考查直线方程的求法，解题时要认真审题，仔细解答，注意点到直线的距离公式和向量知识的合理运用．