题目内容
（本小题满分12分）
设O为坐标原点，点P的坐标
（I）在一个盒子中，放有标号为1，2，3的三张卡片，现从此盒中有放回地先后抽到两张卡片的标号分别记为x，y，求|OP|的最
大值，并求事件“|OP|取到最大值”的概率；
（II）若利用计算机随机在[0，3]上先后取两个数分别记为x，y，求P点在第一象限的概率.
（1）
（2）
解析:
（I）记抽到的卡片标号为（x，y），所有的情况分别为，
| （x，y） | （1，1） | （1，2） | （1，3） | （2，1） | （2，2） | （2，3） | （3，1） | （3，2） | （3，3） |
| P（x-2，x-y） | （-1，0 | （-1，-1） | （-1，-2） | （0，1） | （0，0） | （0，-1） | （1，2） | （1，1） | （1，0）[来源:Z。xx。k.Com] |
| |OP| | 1 |
|
| 1 | 0 | 1 |
|
| 1 |
共9种.由表格可知|OP|的最大值为
…………5分
设事件A为“|OP|取到最大
值”，则满足事件A的（x，y）有（1，3），（3，1）两种情况，
…………7分
（II）设事件B为“P点在第一象限”
|
则其所表示的区域面积为
由题意可得事件B满足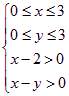
，
即如图所示的阴影部分，
其区域面积为
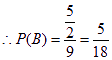…………12分
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
