题目内容
已知函数f(x)=2x+2ax+b,且f(1)= ,f(2)=
,f(2)=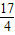 .
.(1)求a、b;
(2)判断f(x)的奇偶性;
(3)试判断函数在(-∞,0]上的单调性,并证明.
【答案】分析:(1)已知条件代入得到关于a,b的方程组,两式相除可得a,把a代入其中一式可得b;
(2)首先判断函数的定义域是否关于原点对称,然后判断f(-x)与f(x)的关系;
(3)利用的单调性定义来证明:设元,作差,变形,判号,下结论.
解答:解:(1)由已知得: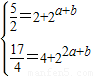 ,解得
,解得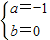 .
.
(2)由(1)知:f(x)=2x+2-x.任取x∈R,则f(-x)=2-x+2-(-x)=f(x),所以f(x)为偶函数.
(3)函数f(x)在(-∞,0]上为减函数.
证明:设x1、x2∈(-∞,0],且x1<x2,则
f(x1)-f(x2)=(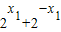 )-(
)-(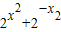 )=(
)=(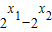 )+(
)+(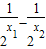 )=
)=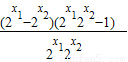
∵x1<x2<0,∴0<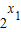 <
<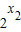 <1,∴
<1,∴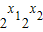 >0,,∴
>0,,∴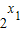 -
-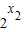 <0,,∴
<0,,∴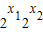 -1<0,
-1<0,
∴f(x1)-f(x2)>0,即f(x1)>f(x2),
∴函数f(x)在(-∞,0]上为减函数.
点评:本题考查了待定系数法求函数解析式,函数的奇偶性、单调性等,注意单调性证明变形要彻底,奇偶性的证明首先判断函数的定义域是否关开原点对称.
(2)首先判断函数的定义域是否关于原点对称,然后判断f(-x)与f(x)的关系;
(3)利用的单调性定义来证明:设元,作差,变形,判号,下结论.
解答:解:(1)由已知得:
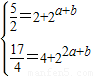 ,解得
,解得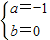 .
.(2)由(1)知:f(x)=2x+2-x.任取x∈R,则f(-x)=2-x+2-(-x)=f(x),所以f(x)为偶函数.
(3)函数f(x)在(-∞,0]上为减函数.
证明:设x1、x2∈(-∞,0],且x1<x2,则
f(x1)-f(x2)=(
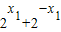 )-(
)-(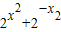 )=(
)=(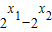 )+(
)+(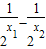 )=
)=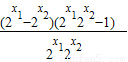
∵x1<x2<0,∴0<
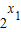 <
<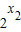 <1,∴
<1,∴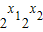 >0,,∴
>0,,∴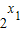 -
-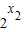 <0,,∴
<0,,∴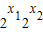 -1<0,
-1<0,∴f(x1)-f(x2)>0,即f(x1)>f(x2),
∴函数f(x)在(-∞,0]上为减函数.
点评:本题考查了待定系数法求函数解析式,函数的奇偶性、单调性等,注意单调性证明变形要彻底,奇偶性的证明首先判断函数的定义域是否关开原点对称.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目