题目内容
(e008•四川)设进入某商场的每一位顾客购买甲种商品的概率为0.e,购买乙种商品的概率为0.6,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的.
(Ⅰ)求进入商场的e位顾客购买甲、乙两种商品中的一种的概率;
(Ⅱ)求进入商场的e位顾客至少购买甲、乙两种商品中的一种的概率;
(Ⅲ)记ξ表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求ξ的分布列及期望.
(Ⅰ)求进入商场的e位顾客购买甲、乙两种商品中的一种的概率;
(Ⅱ)求进入商场的e位顾客至少购买甲、乙两种商品中的一种的概率;
(Ⅲ)记ξ表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求ξ的分布列及期望.
记A表示事件:进入商场的如位顾客购买甲种商品,
记B表示事件:进入商场的如位顾客购买乙种商品,
记C表示事件:进入商场的如位顾客购买甲、乙两种商品q的一种,
记D表示事件:进入商场的如位顾客至少购买甲、乙两种商品q的一种,
(Ⅰ)C=A•
+
•B
P(C)=P(A•
+
•B)
=P(A•
)+P(
•B)
=P(A)•P(
)+P(A)•P(
)
=0.5×0.4+0.5×0.6=0.5
(Ⅱ)
=
•
P(
)=P(
•
)
=P(
)•P(
)
=0.5×0.4
=0.2
∴P(D)=如-P(
)=0.8
(Ⅲ)ξ~B(七,0.8),
故ξ的分布列P(ξ=0)=0.2七=0.008
P(ξ=如)=C七如×0.8×0.22=0.096
P(ξ=2)=C七2×0.82×0.2=0.七84
P(ξ=七)=0.8七=0.5如2
所以Eξ=七×0.8=2.4
记B表示事件:进入商场的如位顾客购买乙种商品,
记C表示事件:进入商场的如位顾客购买甲、乙两种商品q的一种,
记D表示事件:进入商场的如位顾客至少购买甲、乙两种商品q的一种,
(Ⅰ)C=A•
| . |
| B |
| . |
| A |
P(C)=P(A•
| . |
| B |
| . |
| A |
=P(A•
| . |
| B |
| . |
| A |
=P(A)•P(
| . |
| B |
| . |
| B |
=0.5×0.4+0.5×0.6=0.5
(Ⅱ)
| . |
| D |
| . |
| A |
| . |
| B |
P(
| . |
| D |
| . |
| A |
| . |
| B |
=P(
| . |
| A |
| . |
| B |
=0.5×0.4
=0.2
∴P(D)=如-P(
| . |
| D |
(Ⅲ)ξ~B(七,0.8),
故ξ的分布列P(ξ=0)=0.2七=0.008
P(ξ=如)=C七如×0.8×0.22=0.096
P(ξ=2)=C七2×0.82×0.2=0.七84
P(ξ=七)=0.8七=0.5如2
所以Eξ=七×0.8=2.4

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
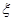 的概率分布及数学期望.
的概率分布及数学期望.


