题目内容
已知点A(-2,0),B(2,0),直线AP与直线BP相交于点P,它们的斜率之积为 ,求点P的轨迹方程(化为标准方程).
,求点P的轨迹方程(化为标准方程).
解:设P(x,y),因为A(-2,0),B(2,0)
所以kAP=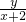 (x≠-2),kBP=
(x≠-2),kBP=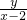 (x≠2)
(x≠2)
由已知, (x≠±2)
(x≠±2)
化简,得 (x≠±2)
(x≠±2)
点P的轨迹方程: (x≠±2).
(x≠±2).
分析:设出点P的坐标,表示出直线AM、BM的斜率,求出它们的斜率之积,利用斜率之积是 ,建立方程,去掉不满足条件的点,即可得到点M的轨迹方程.
,建立方程,去掉不满足条件的点,即可得到点M的轨迹方程.
点评:本题重点考查轨迹方程的求解,解题的关键是正确表示出直线AM、BM的斜率,利用条件建立方程.
所以kAP=
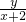 (x≠-2),kBP=
(x≠-2),kBP=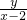 (x≠2)
(x≠2)由已知,
 (x≠±2)
(x≠±2)化简,得
 (x≠±2)
(x≠±2)点P的轨迹方程:
 (x≠±2).
(x≠±2).分析:设出点P的坐标,表示出直线AM、BM的斜率,求出它们的斜率之积,利用斜率之积是
 ,建立方程,去掉不满足条件的点,即可得到点M的轨迹方程.
,建立方程,去掉不满足条件的点,即可得到点M的轨迹方程.点评:本题重点考查轨迹方程的求解,解题的关键是正确表示出直线AM、BM的斜率,利用条件建立方程.

练习册系列答案
相关题目