题目内容
若存在实常数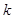 和
和 ,使得函数
,使得函数 和
和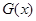 对其公共定义域上的任意实数
对其公共定义域上的任意实数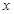 都满足:
都满足: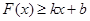 和
和 恒成立,则称此直线
恒成立,则称此直线 为
为 和
和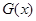 的“隔离直线”.已知函数
的“隔离直线”.已知函数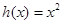 ,
, 为自然对数的底数),
为自然对数的底数), ,
,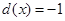 .有下列命题:①
.有下列命题:① 在
在 递减;②
递减;②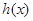 和
和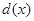 存在唯一的“隔离直线”;③
存在唯一的“隔离直线”;③ 和
和 存在“隔离直线”
存在“隔离直线” ,且
,且 的最大值为
的最大值为 ;④函数
;④函数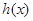 和
和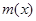 存在唯一的隔离直线
存在唯一的隔离直线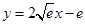 .其中真命题的个数
.其中真命题的个数
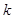 和
和 ,使得函数
,使得函数 和
和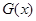 对其公共定义域上的任意实数
对其公共定义域上的任意实数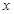 都满足:
都满足: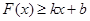 和
和 恒成立,则称此直线
恒成立,则称此直线 为
为 和
和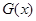 的“隔离直线”.已知函数
的“隔离直线”.已知函数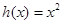 ,
, 为自然对数的底数),
为自然对数的底数), ,
,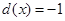 .有下列命题:①
.有下列命题:① 在
在 递减;②
递减;②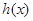 和
和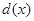 存在唯一的“隔离直线”;③
存在唯一的“隔离直线”;③ 和
和 存在“隔离直线”
存在“隔离直线” ,且
,且 的最大值为
的最大值为 ;④函数
;④函数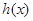 和
和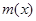 存在唯一的隔离直线
存在唯一的隔离直线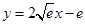 .其中真命题的个数
.其中真命题的个数 A.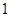 个 个 | B. 个 个 | C. 个 个 | D.个 |
C
①:由已知得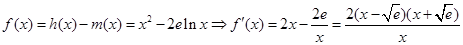 ,当
,当 ,且
,且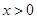 时,得到
时,得到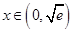 ,所以该函数在
,所以该函数在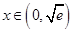 上递减,所以正确;②由已知得到,
上递减,所以正确;②由已知得到,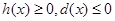 ,所以隔离直线由许多条,只要满足
,所以隔离直线由许多条,只要满足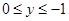 即可,所以错误;
即可,所以错误;
③由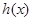 和
和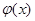 可知,函数有许多隔离直线,函数
可知,函数有许多隔离直线,函数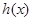 与
与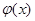 平行的切线方程为
平行的切线方程为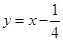 ,所以且
,所以且 的最大值为
的最大值为 ;最小值为-2;所以正确;④证明出
;最小值为-2;所以正确;④证明出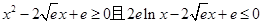 即可,所以正确;所以选C
即可,所以正确;所以选C
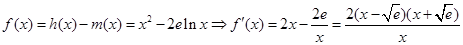 ,当
,当 ,且
,且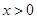 时,得到
时,得到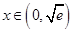 ,所以该函数在
,所以该函数在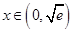 上递减,所以正确;②由已知得到,
上递减,所以正确;②由已知得到,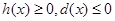 ,所以隔离直线由许多条,只要满足
,所以隔离直线由许多条,只要满足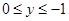 即可,所以错误;
即可,所以错误;③由
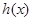 和
和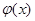 可知,函数有许多隔离直线,函数
可知,函数有许多隔离直线,函数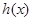 与
与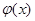 平行的切线方程为
平行的切线方程为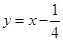 ,所以且
,所以且 的最大值为
的最大值为 ;最小值为-2;所以正确;④证明出
;最小值为-2;所以正确;④证明出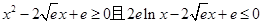 即可,所以正确;所以选C
即可,所以正确;所以选C
练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目
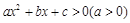 过程的流程图(如图所示),其中①处应填___________。
过程的流程图(如图所示),其中①处应填___________。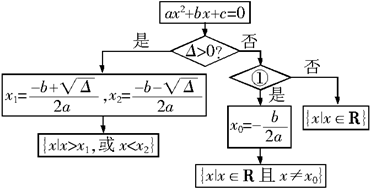
 ,归纳出所有三角形的内角和都是
,归纳出所有三角形的内角和都是 ,五边形内角和是
,五边形内角和是 ,由此得凸多边形内角和是
,由此得凸多边形内角和是
 ,若
,若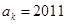 ,则
,则 .
.
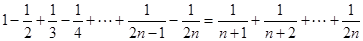 时,从
时,从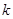 到
到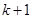 时,等式左边所要添加的项是( )
时,等式左边所要添加的项是( ) 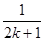
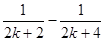
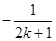
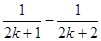
 等于( )
等于( )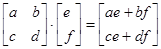 ,如
,如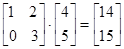 ,已知
,已知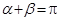 ,
,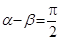 ,则
,则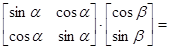 ( )
( )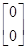
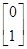
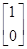
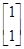
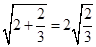 ,
,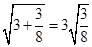 ,
,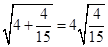 ,。。。,若
,。。。,若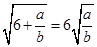 (a , b
(a , b ) , 则( )
) , 则( )