题目内容
已知幂函数f（x）=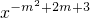
（m∈Z）为偶函数，且在区间（0，+∞）为增函数．求函数f（x）的解析式．
解：由题意可得
解得m=1
∴f（x）=x4
分析：根据幂函数在区间（0，+∞）为增函数可得幂指数大于0，再根据偶函数可得幂指数为偶数，从而可求出m，即可得到函数f（x）的解析式．
点评：本题主要考查了幂函数的性质，以及函数解析式的求法，同时考查了一元二次不等式的解法，属于基础题．
解得m=1
∴f（x）=x4
分析：根据幂函数在区间（0，+∞）为增函数可得幂指数大于0，再根据偶函数可得幂指数为偶数，从而可求出m，即可得到函数f（x）的解析式．
点评：本题主要考查了幂函数的性质，以及函数解析式的求法，同时考查了一元二次不等式的解法，属于基础题．
练习册系列答案
相关题目