题目内容
【题目】已知二次函数![]() 满足
满足![]() (
(![]() ),且
),且![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有唯一实数根,求实数
上有唯一实数根,求实数![]() 的取值范围(注:相等的实数根算一个).
的取值范围(注:相等的实数根算一个).
(3)函数![]() ,试问是否存在实数
,试问是否存在实数![]() ,使得对任意
,使得对任意![]() ,
, ![]() 都有
都有![]() 成立,若存在,求出实数
成立,若存在,求出实数![]() 的取值范围,若不存在,说明理由.
的取值范围,若不存在,说明理由.
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)答案见解析.
;(3)答案见解析.
【解析】试题分析:(1)设![]() (
(![]() ),代入条件化简并根据恒等式成立条件得
),代入条件化简并根据恒等式成立条件得![]() ,
, ![]() ,
, ![]() ,(2)研究二次方程根的情况,往往结合二次函数图像,即转化为研究直线与二次函数交点个数,作出图像,根据图像得实数
,(2)研究二次方程根的情况,往往结合二次函数图像,即转化为研究直线与二次函数交点个数,作出图像,根据图像得实数![]() 的取值范围(3)先将不等式恒成立问题转化为对应函数最值:
的取值范围(3)先将不等式恒成立问题转化为对应函数最值: ![]() ,再根据二次函数对称轴与定义区间位置关系,分类讨论函数最值,解对应不等式,可得实数
,再根据二次函数对称轴与定义区间位置关系,分类讨论函数最值,解对应不等式,可得实数![]() 的取值范围
的取值范围
试题解析:(1)设![]() (
(![]() )
)
代入![]() 得
得![]() 对于
对于![]() 恒成立,故
恒成立,故![]()
又由![]() 得
得![]() ,解得
,解得![]() ,
, ![]() ,
, ![]() ,
,
所以![]()
(2)由方程![]() 得
得![]() ,令
,令![]() ,
, ![]() ,
,
即要求函数![]() 在
在![]() 上有唯一的零点,
上有唯一的零点,
①![]() ,则
,则![]() ,代入原方程得
,代入原方程得![]() 或
或![]() ,不合题意;
,不合题意;
②若![]() ,则
,则![]() ,代入原方程得
,代入原方程得![]() 或
或![]() ,满足题意,故
,满足题意,故![]() 成立;
成立;
③若![]() ,则
,则![]() ,代入原方程得
,代入原方程得![]() ,满足题意,故
,满足题意,故![]() 成立.
成立.
④若![]() 且
且![]() 且
且![]() 时,由
时,由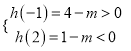 得
得![]() .
.
综上,实数![]() 的取值范围是
的取值范围是![]() .
.
解法2:由方程![]() 得
得![]() ,即直线
,即直线![]() 与函数
与函数![]() ,
, ![]() 的图象有且只有一个交点(参照给分)
的图象有且只有一个交点(参照给分)
(3)由题意知![]()
假设存在实数![]() 满足条件,对任意
满足条件,对任意![]() ,
, ![]() 都有
都有![]() 成立,即
成立,即![]() ,故有
,故有![]() ,
,
由![]() ,
, ![]()
①当![]() 时,
时, ![]() 在
在![]() 上为增函数
上为增函数![]() ,
, ![]() ,所以
,所以![]()
②当![]() 时,
时, ![]()
![]() ,即
,即![]()
解得![]() ,所以
,所以![]() .
.
③当![]() 时,
时, ![]()
即![]() 解得
解得![]() ,所以
,所以![]()
③当![]() 时,
时, ![]()
即![]() ,所以
,所以![]()
综上所述, ![]()
所以当![]() 时,使得对任意
时,使得对任意![]() ,
, ![]() 都有
都有![]() 成立
成立

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目