题目内容
已知函数f(x)=Asin(ωx+φ)(其中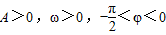 )的相邻对称轴之间的距离为
)的相邻对称轴之间的距离为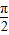 ,且该函数图象的一个最高点为
,且该函数图象的一个最高点为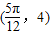 .
.(1)求函数f(x)的解析式和单调增区间;
(2)若
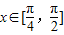 ,求函数f(x)的最大值和最小值.
,求函数f(x)的最大值和最小值.
【答案】分析:(1)根据已知条件,我们可以分析出函数的最值及周期,进而求出A和ω,代入最大值点坐标,结合φ的范围,求出φ值,可得f(x)的解析式结合正弦函数的单调性,可求出函数的单调增区间;
(2)由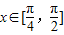 可得相位角2x-
可得相位角2x-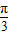 的取值范围,结合正弦函数的图象和性质可得函数f(x)的值域,进而求出其最值.
的取值范围,结合正弦函数的图象和性质可得函数f(x)的值域,进而求出其最值.
解答:解:(1)由题意,函数图象的一个最高点为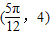 ,则A=4,
,则A=4,
又∵相邻对称轴之间的距离为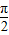 ,即
,即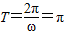 ,得ω=2,
,得ω=2,
所以f(x)=4sin(2x+φ),…(2分)
再由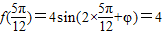 ,且
,且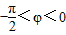 ,
,
得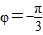 ,
,
所以f(x)的解析式为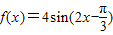 .…(4分)
.…(4分)
由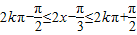 ,…(6分)
,…(6分)
得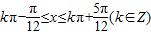 ,
,
所以f(x)的单调增区间为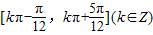 .…(8分)
.…(8分)
(2)因为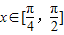 ,
,
所以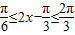 ,…(10分)
,…(10分)
所以,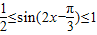 ,…(12分)
,…(12分)
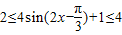 ,
,
所以f(x)max=4,f(x)min=2.…(16分)
点评:本题考查的知识点是正弦型函数的图象和性质,由函数的图象求函数的解析式,熟练掌握正弦型函数的图象和性质是解答的关键.
(2)由
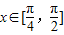 可得相位角2x-
可得相位角2x-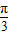 的取值范围,结合正弦函数的图象和性质可得函数f(x)的值域,进而求出其最值.
的取值范围,结合正弦函数的图象和性质可得函数f(x)的值域,进而求出其最值.解答:解:(1)由题意,函数图象的一个最高点为
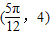 ,则A=4,
,则A=4,又∵相邻对称轴之间的距离为
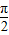 ,即
,即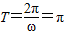 ,得ω=2,
,得ω=2,所以f(x)=4sin(2x+φ),…(2分)
再由
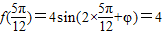 ,且
,且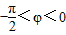 ,
,得
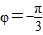 ,
,所以f(x)的解析式为
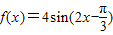 .…(4分)
.…(4分)由
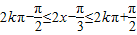 ,…(6分)
,…(6分)得
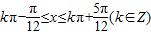 ,
,所以f(x)的单调增区间为
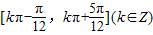 .…(8分)
.…(8分)(2)因为
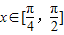 ,
,所以
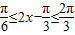 ,…(10分)
,…(10分)所以,
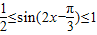 ,…(12分)
,…(12分)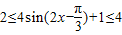 ,
,所以f(x)max=4,f(x)min=2.…(16分)
点评:本题考查的知识点是正弦型函数的图象和性质,由函数的图象求函数的解析式,熟练掌握正弦型函数的图象和性质是解答的关键.

练习册系列答案
相关题目