题目内容
如图,所有棱长都为2的正三棱柱BCD-B′C′D′,四边形ABCD是菱形,其中E为BD的中点.
(1)求证:C′E∥面AB′D′;
(2)求面AB'D'与面ABD所成锐二面角的余弦值;
(3)求四棱锥B'-ABCD与D'-ABCD的公共部分体积.

(1)求证:C′E∥面AB′D′;
(2)求面AB'D'与面ABD所成锐二面角的余弦值;
(3)求四棱锥B'-ABCD与D'-ABCD的公共部分体积.

证明:(1)如图取B'D'的中点为F,连AF,C′F,
易得AFC′F为平行四边形.
∴AF∥C'E,
又AF?平面AB′D′,
∴C′E∥面AB′D′..(4分)
(2)因ABCD为菱形,且∠DCB=60°,取BC中点为G
易得AD,DG,DD’相互垂直,故分别以之为x,y,z轴建立坐标系如图.
由棱长为2得A(2,0,0),B′(1,
,2),D′(0,0,2)
进而得面ADD'的一个法向量为(1,-
,1),又面ABD的法向量为(0,0,1)
所以面AB'D'与面ABD所成锐二面角的余弦值
cosθ=
=
(3)设B’D与BD的交点为O,
由图得四棱锥B'-ABCD与D'-ABCD的公共部分为四棱锥O-ABCD,
且O到下底面的距离为1,
SABCD=2×
×2×2sin600=2
所以公共部分的体积为
×2
×1=
.

易得AFC′F为平行四边形.
∴AF∥C'E,
又AF?平面AB′D′,
∴C′E∥面AB′D′..(4分)
(2)因ABCD为菱形,且∠DCB=60°,取BC中点为G
易得AD,DG,DD’相互垂直,故分别以之为x,y,z轴建立坐标系如图.
由棱长为2得A(2,0,0),B′(1,
| 3 |
进而得面ADD'的一个法向量为(1,-
| ||
| 3 |
所以面AB'D'与面ABD所成锐二面角的余弦值
cosθ=
(1,-
| ||||
|
| ||
| 7 |
(3)设B’D与BD的交点为O,
由图得四棱锥B'-ABCD与D'-ABCD的公共部分为四棱锥O-ABCD,
且O到下底面的距离为1,
SABCD=2×
| 1 |
| 2 |
| 3 |
所以公共部分的体积为
| 1 |
| 3 |
| 3 |
2
| ||
| 3 |


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
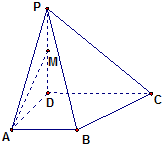


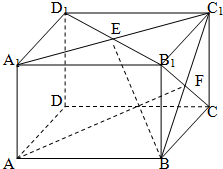

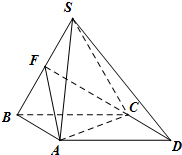
 ABCD中,错误的式子是( )
ABCD中,错误的式子是( ) 

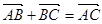

 =a,
=a, =b,
=b, ,用a,b表示
,用a,b表示 ,则
,则
 b
b a+
a+