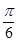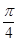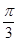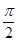题目内容
在锐角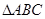 中,角A,B,C所对的边分别是
中,角A,B,C所对的边分别是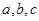 ,且
,且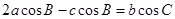 。
。
(Ⅰ)求B;
(Ⅱ)若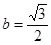 ,求周长
,求周长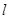 的最大值。
的最大值。
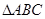 中,角A,B,C所对的边分别是
中,角A,B,C所对的边分别是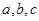 ,且
,且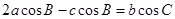 。
。(Ⅰ)求B;
(Ⅱ)若
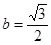 ,求周长
,求周长 的最大值。
的最大值。(Ⅰ) (Ⅱ)
(Ⅱ)
 (Ⅱ)
(Ⅱ)
本试题主要是考查了解三角形的运用,以及三角函数性质的综合运用
(1)由于函数中利用正弦定理化边为角,然后解方程得到角。
(2)同时在第一问的基础上,所求的边化为关于A的单一函数,结合定义域得到值域。
解:(Ⅰ)由
得 , 1分
, 1分
即 , 2分
, 2分
所以 3分
3分
 ; 4分
; 4分
(Ⅱ)由正弦定理,得 , 5分
, 5分
又 ,则
,则 ,
,

 , 6分
, 6分
因为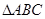 是锐角三角形,所以
是锐角三角形,所以 ,即
,即 , 7分
, 7分
 ,所以
,所以 最大值为
最大值为 8分
8分
(1)由于函数中利用正弦定理化边为角,然后解方程得到角。
(2)同时在第一问的基础上,所求的边化为关于A的单一函数,结合定义域得到值域。
解:(Ⅰ)由

得
 , 1分
, 1分即
 , 2分
, 2分所以
 3分
3分 ; 4分
; 4分(Ⅱ)由正弦定理,得
 , 5分
, 5分又
 ,则
,则 ,
,
 , 6分
, 6分因为
 是锐角三角形,所以
是锐角三角形,所以 ,即
,即 , 7分
, 7分 ,所以
,所以 最大值为
最大值为 8分
8分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,已知
中,已知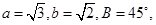 求
求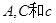 .
. 中 ,角
中 ,角 的对边分别为
的对边分别为 ,且满足
,且满足 。若
。若 。求此三角形的面积;
。求此三角形的面积; 中,已知
中,已知 ,
, ,试判断
,试判断 则ΔABC的面积为 .
则ΔABC的面积为 .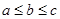 ),设向量
),设向量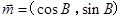 ,
,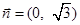 ,且向量
,且向量 为单位向量.(模为1的向量称作单位向量)
为单位向量.(模为1的向量称作单位向量) ,求△ABC的面积.
,求△ABC的面积. 中,
中, ,且
,且 ,则
,则 是
是 中
中 所对的边,如果
所对的边,如果 ,那么
,那么 等于( )
等于( )


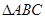 中,若
中,若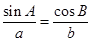 ,则角B为( )
,则角B为( )