Question

如图,四棱锥P—ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,BC=,E、F分别为AD、PC的中点.

(1)求证:PC⊥平面BEF;

(2)求BD与平面BEF所成角的正弦值.

Answer 1

解法一:(1)证明:∵PA⊥底面ABCD,AB平面ABCD,

∴PA⊥AB.

∴PB==BC.

又F为PC的中点,∴BF⊥PC.

连结PE、EC,同理,得PE=.

∵E为AD的中点,∴EC=.

∴PE=CE.∴EF⊥PC.

∵BF∩EF=F,∴PC⊥平面BEF.

(2)解:∵PC⊥平面BEF,CF平面CEF,

∴平面CEF⊥平面BEF.

设EC交BD于点M,过M作MN∥CF交EF于点N,则MN⊥平面BEF.

连结BN,则∠MBN为BD与平面BEF所成的角.

由△DEM∽△BCM可知,BM=2DM=BD=,EM=EC,

由△EMN∽△ECF可知,MN=FC=PC,

又△PBC是等腰三角形,∴PC==2.

∴MN=PC=.∴sin∠MBN=.

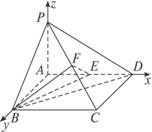
解法二:以A为坐标原点,以射线AD、AB、AP分别为x轴、y轴、z轴建立空间直角坐标系,则P(0,0,1),B(0,1,0),C(,1,0),D(,0,0),E(,0,0),F(, ,).

(1)证明:=(,1,-1), =(,-,),EF=(0, ,),

∴·=0, ·=0.

∴PC⊥BF,PC⊥EF.

又BF平面BEF,EF平面BEF,BF∩EF=F,

∴PC⊥平面BEF.

(2)解:∵=（,-1,0),PC=(,1,-1),

cos〈,〉=.

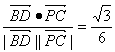∵PC⊥平面BEF,

∴是平面BEF的法向量.

∴BD与平面BEF所成角的正弦值即为.