题目内容
 设全集U=R,A={y|y=tanx,x∈B},B={x||x|≤
设全集U=R,A={y|y=tanx,x∈B},B={x||x|≤ },则图中阴影部分表示的集合是
},则图中阴影部分表示的集合是
- A.[-1,1]
- B.[-
 ,
, ]
] - C.[-1,-
 )∪(
)∪( ,1]
,1] - D.[-1,-
 ]∪[
]∪[ ,1]
,1]
C
分析:图中阴影部分所表示的集合是A∩(CUB),由全集U=R,B={x||x|≤ }={x|-
}={x|-
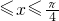 },知A={y|y=tanx,x∈B}={y|-1≤y≤1},由此能求出图中阴影部分表示的集合.
},知A={y|y=tanx,x∈B}={y|-1≤y≤1},由此能求出图中阴影部分表示的集合.
解答:∵阴影部分对应的集合,它的元素在集合A内,
∴所求集合的元素必定为集合A的元素,
又∵阴影部分对应的集合,它的元素不在集合B内,
∴所求集合的元素必定不是集合B的元素,应该在B的补集当中.
故图中阴影部分所表示的集合是A∩(CUB),
∵全集U=R,B={x||x|≤ }={x|-
}={x|-
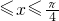 },
},
∴A={y|y=tanx,x∈B}={y|-1≤y≤1},
∴A∩(CUB)=[-1,- )∪(
)∪( ,1].
,1].
故选C.
点评:本题根据图形中阴影部分,让我们找出它所表示的集合,着重考查了Venn图表达集合的关系及运算,考查了数形结合的思想,属于基础题.
分析:图中阴影部分所表示的集合是A∩(CUB),由全集U=R,B={x||x|≤
 }={x|-
}={x|-
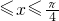 },知A={y|y=tanx,x∈B}={y|-1≤y≤1},由此能求出图中阴影部分表示的集合.
},知A={y|y=tanx,x∈B}={y|-1≤y≤1},由此能求出图中阴影部分表示的集合.解答:∵阴影部分对应的集合,它的元素在集合A内,
∴所求集合的元素必定为集合A的元素,
又∵阴影部分对应的集合,它的元素不在集合B内,
∴所求集合的元素必定不是集合B的元素,应该在B的补集当中.
故图中阴影部分所表示的集合是A∩(CUB),
∵全集U=R,B={x||x|≤
 }={x|-
}={x|-
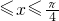 },
},∴A={y|y=tanx,x∈B}={y|-1≤y≤1},
∴A∩(CUB)=[-1,-
 )∪(
)∪( ,1].
,1].故选C.
点评:本题根据图形中阴影部分,让我们找出它所表示的集合,着重考查了Venn图表达集合的关系及运算,考查了数形结合的思想,属于基础题.

练习册系列答案
相关题目
设全集U=R,A={x|ax+1=0},B={1,2},若A∩(?UB)=?,则实数a的取值集合是( )
| A、{0} | ||
| B、? | ||
C、{-1,-
| ||
D、{-1,-
|