题目内容
已知函数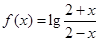 .
.
(1)求函数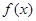 的定义域;
的定义域;
(2)判定函数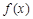 的奇偶性,并加以证明;
的奇偶性,并加以证明;
(3)判定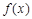 的单调性,并求不等式
的单调性,并求不等式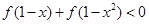 的解集.
的解集.
【答案】
(1) (-2,2)(2)奇函数(3)
【解析】
试题分析:解:(1). ,所以函数f(x)的定义域为:(-2,2)
4分
,所以函数f(x)的定义域为:(-2,2)
4分
(2).任取x∈(-2,2),有 ,所以函数f(x)是奇函数..8分
,所以函数f(x)是奇函数..8分
(3).∵ 在(-2,2)上单调递增,∴f(x)=
在(-2,2)上单调递增,∴f(x)=
在(-2,2)上单调递增(只要判断正确,就给1分) 9分
所以 10分
10分
∴原不等式 12分
12分
所以不等式的解集为: .(或(1,
.(或(1, ))
13分
))
13分
考点:函数的单调性和奇偶性
点评:解决的关键是根据函数的概念和性质来分析得到,属于基础题。

练习册系列答案
相关题目
 .
. 的单调区间;
的单调区间; ,
, 在区间
在区间 恒成立,求a的取值范围.
恒成立,求a的取值范围. ,
,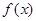 的单调递减区间;
的单调递减区间; 时,求函数
时,求函数 .
. .
. 的单调区间;
的单调区间; 时,判断
时,判断 和
和 的大小,并说明理由;
的大小,并说明理由; 时,关于
时,关于 的方程:
的方程: 在区间
在区间 上总有两个不同的解.
上总有两个不同的解. ,
,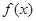 的最小值;
的最小值; 都有
都有 ,求实数
,求实数 的取值范围.
的取值范围.