题目内容
如图所示,某人沿着网格线前进,他走最短路线: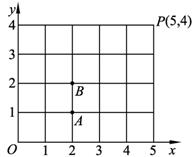
(1)这人从原点O(0,0)走到点P(5,4)可有多少条不同的行走路线?
(2)若擦去从点A(2,1)到点B(2,2)这一段,也就是假设这一段禁止通行,这个人又有多少条不同的行走路线?
解析:(1)这人从原点O(0,0)走到点P(5,4),必须向右行走5个单位,向上行走4个单位,这样任何一条行走路线都一一对应于从5+4个单位中选取4个位置向上走,无论向上走的4个位置排在9个单位中哪个位置上,共有![]() =126条路线.
=126条路线.
(2)由(1)知,这人从原点O(0,0)走到A(2,1)的最短路线有![]() 条,从点A(2,1)到点B(2,2)的最短路线则是唯一的,又从点B(2,2)到点P(5,4)的最短路线有
条,从点A(2,1)到点B(2,2)的最短路线则是唯一的,又从点B(2,2)到点P(5,4)的最短路线有![]() 条.所以,这人不走AB这一段,从原点O(0,0)走到点P(5,4)的最短路线有:
条.所以,这人不走AB这一段,从原点O(0,0)走到点P(5,4)的最短路线有:
![]() -
-![]()
![]() =96(条).
=96(条).

练习册系列答案
相关题目

 如图所示,某人拨通了电话,准备手机充值须如下操作( )
如图所示,某人拨通了电话,准备手机充值须如下操作( ) 一个旅游景区的游览线路如图所示,某人从点P处进,Q点处出,沿图中线路游览A、B、C三个景点及沿途风景,则不重复(除交汇点O外)的不同游览线路有( )种.
一个旅游景区的游览线路如图所示,某人从点P处进,Q点处出,沿图中线路游览A、B、C三个景点及沿途风景,则不重复(除交汇点O外)的不同游览线路有( )种.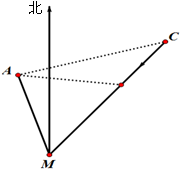 如图所示,某人在M汽车站的北偏西20°的方向上的A处,观察到点C处有一辆汽车沿公路向M站行驶,公路的走向是M站的北偏东40°,开始时,汽车到A的距离为31千米,汽车前进20千米后,到A的距离缩短了10千米.问汽车还需行驶多远,才能到达M汽车站?
如图所示,某人在M汽车站的北偏西20°的方向上的A处,观察到点C处有一辆汽车沿公路向M站行驶,公路的走向是M站的北偏东40°,开始时,汽车到A的距离为31千米,汽车前进20千米后,到A的距离缩短了10千米.问汽车还需行驶多远,才能到达M汽车站?