题目内容
如图所示,在一个特定时段内,以点E为中心的10海里以内海域被设为警戒水域.点E正北40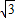 海里处有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东30°且与点A相距100海里的位置B,经过2小时又测得该船已行驶到点A北偏东60°且与点A相距20
海里处有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东30°且与点A相距100海里的位置B,经过2小时又测得该船已行驶到点A北偏东60°且与点A相距20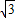 海里的位置C.
海里的位置C.(1)求该船的行驶速度(单位:海里/小时);
(2)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域,并说明理由.
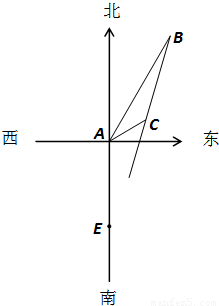
【答案】分析:(Ⅰ)先以点A为原点,正东方向为X轴正半轴建系如图,得出点B,C的坐标,再利用两点距离公式得BC从而求得小船速度即可;
(Ⅱ)欲判断它是否会进入警戒水域,只须比较圆心E到直线BC的距离圆的半径的大小即可.
解答:解析:(1)如图建立平面直角坐标系:设一个单位为10海里
则坐标平面中AB=10,AC=2 A(0,0),E(0,-4
A(0,0),E(0,-4 )
)
再由方位角可求得:B(5,5 ),C(3,
),C(3, )
)
…4分
所以|BC|= =2
=2
…6分
所以BC两地的距离为20 海里
海里
所以该船行驶的速度为10 海里/小时
海里/小时
…7分
(2)直线BC的斜率为 =2
=2
所以直线BC的方程为:y- =2
=2 (x-3)
(x-3)
即2 x-y-5
x-y-5 =0…10分
=0…10分
所以E点到直线BC的距离为 =
= <1…12分
<1…12分
所以直线BC会与以E为圆心,以一个单位长为半径的圆相交,
所以若该船不改变航行方向则会进入警戒水域.…14分
答:该船行驶的速度为10 海里/小时,若该船不改变航行方向则会进入警戒水域.
海里/小时,若该船不改变航行方向则会进入警戒水域.
点评:本题考查已三角函数模型的应用问题,注意选择正确的坐标系以及合理的定理解答是解好题目的关键,考查计算能力.
(Ⅱ)欲判断它是否会进入警戒水域,只须比较圆心E到直线BC的距离圆的半径的大小即可.
解答:解析:(1)如图建立平面直角坐标系:设一个单位为10海里
则坐标平面中AB=10,AC=2
 A(0,0),E(0,-4
A(0,0),E(0,-4 )
)再由方位角可求得:B(5,5
 ),C(3,
),C(3, )
)…4分
所以|BC|=
 =2
=2
…6分
所以BC两地的距离为20
 海里
海里所以该船行驶的速度为10
 海里/小时
海里/小时…7分
(2)直线BC的斜率为
 =2
=2
所以直线BC的方程为:y-
 =2
=2 (x-3)
(x-3)即2
 x-y-5
x-y-5 =0…10分
=0…10分所以E点到直线BC的距离为
 =
= <1…12分
<1…12分所以直线BC会与以E为圆心,以一个单位长为半径的圆相交,
所以若该船不改变航行方向则会进入警戒水域.…14分
答:该船行驶的速度为10
 海里/小时,若该船不改变航行方向则会进入警戒水域.
海里/小时,若该船不改变航行方向则会进入警戒水域.点评:本题考查已三角函数模型的应用问题,注意选择正确的坐标系以及合理的定理解答是解好题目的关键,考查计算能力.

练习册系列答案
相关题目
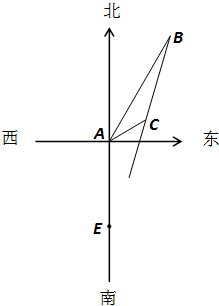 如图所示,在一个特定时段内,以点E为中心的10海里以内海域被设为警戒水域.点E正北40
如图所示,在一个特定时段内,以点E为中心的10海里以内海域被设为警戒水域.点E正北40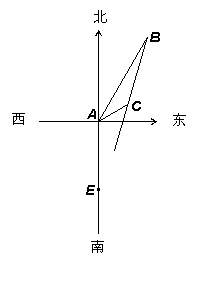
 海里处有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东30°且与点A相距100海里的位置B,经过2小时又测得该船已行驶到点A北偏东60°且与点A相距20
海里处有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东30°且与点A相距100海里的位置B,经过2小时又测得该船已行驶到点A北偏东60°且与点A相距20