题目内容
(本小题满分12分)
双曲线 与双曲线
与双曲线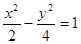 有共同的渐近线,且经过点
有共同的渐近线,且经过点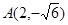 ,椭圆
,椭圆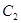 以双曲线
以双曲线 的焦点为焦点且椭圆上的点与焦点的最短距离为
的焦点为焦点且椭圆上的点与焦点的最短距离为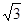 ,求双曲线
,求双曲线 和椭圆
和椭圆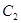 的方程。
的方程。
 ,
,
解析试题分析:解:由已知设双曲线方程
∵过

则焦点 。 设椭圆方程
。 设椭圆方程
椭圆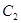 上任意一点
上任意一点



考点:本试题考查了双曲线和椭圆方程的知识。
点评:解决该试题的关键是对于椭圆和双曲线的性质的准确表示和方程的准确求解。利用已知中的条件,会设公共渐近线的双曲线的方程即为 ,只要将右边的系数改为一个固定的参数即可,这个知识点要掌握,属于中档题。
,只要将右边的系数改为一个固定的参数即可,这个知识点要掌握,属于中档题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
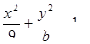 的右焦点F2重合,F1是椭圆的左焦点;
的右焦点F2重合,F1是椭圆的左焦点;  ABC中,若A(-4,0),B(0,-3),点C在抛物线y2=4x上运动,求
ABC中,若A(-4,0),B(0,-3),点C在抛物线y2=4x上运动,求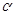 ,∠PF2F1=
,∠PF2F1=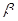 ,求cos
,求cos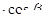 的值及
的值及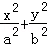 =1(a>b>0)的两个焦点分别为F1(﹣c,0),F2(c,0),M是椭圆短轴的一个端点,且满足
=1(a>b>0)的两个焦点分别为F1(﹣c,0),F2(c,0),M是椭圆短轴的一个端点,且满足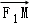
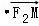 =0,点N( 0,3 )到椭圆上的点的最远距离为5
=0,点N( 0,3 )到椭圆上的点的最远距离为5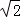
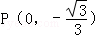 ;问A、B两点能否关于过点P、Q的直线对称?若能,求出k的取值范围;若不能,请说明理由.
;问A、B两点能否关于过点P、Q的直线对称?若能,求出k的取值范围;若不能,请说明理由. 的离心率为
的离心率为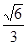 ,
, 为椭圆的右焦点,
为椭圆的右焦点,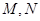 两点在椭圆
两点在椭圆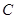 上,且
上,且 ,定点
,定点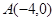 。
。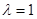 时,有
时,有 ,求椭圆
,求椭圆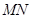 斜率为k,且设
斜率为k,且设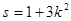 时,试求
时,试求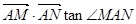 关于S的函数表达式f(s)的最大值,以及此时
关于S的函数表达式f(s)的最大值,以及此时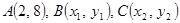 在抛物线
在抛物线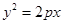 上,
上, 的重心与此抛物线的焦点F重合。
的重心与此抛物线的焦点F重合。 相切。记动点P的轨迹为C。
相切。记动点P的轨迹为C。 与直线4x+3y + 1 =0相切,动圆M与
与直线4x+3y + 1 =0相切,动圆M与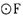 及y轴都相切. (I )求点M的轨迹C的方程;(II)过点F任作直线l,交曲线C于A,B两点,由点A,B分别向
及y轴都相切. (I )求点M的轨迹C的方程;(II)过点F任作直线l,交曲线C于A,B两点,由点A,B分别向 各引一条切线,切点 分别为P,Q,记
各引一条切线,切点 分别为P,Q,记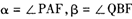 .求证
.求证 是定值.
是定值.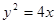 及点
及点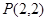 ,直线
,直线 的斜率为1且不过点P,与抛物线交于A,B两点。
的斜率为1且不过点P,与抛物线交于A,B两点。 轴上截距的取值范围;
轴上截距的取值范围; 、
、 两个岛屿,
两个岛屿, ,曾有渔船在距
,曾有渔船在距 轴,
轴, 的垂直平分线为
的垂直平分线为 轴建立平面直角坐标系。
轴建立平面直角坐标系。
 处反射信号的时间比为
处反射信号的时间比为 ,问你能否确定
,问你能否确定