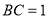题目内容
已知
、
分别是椭圆
的左、右焦点.
（1）若
是第一象限内该椭圆上的一点，
，求点的坐标；
（2）设过定点
的直线
与椭圆交于不同的两点
、
，且
为锐角（其
中
为坐标原点），求直线
的斜率
的取值范围.
（1）点
的坐标为
；（2）直线
的斜率
的取值范围是
.
【解析】
试题分析：（1）设
，由椭圆方程可表示出
、
，又
，即可求点的坐标；
（2）显然
不满足题意，所直线的斜率存在，可设
的方程为
，与椭圆方程联立后用韦达定理表示出
、
；又
为锐角，
，进而可解出
的取值范围.
试题解析：（1）因为椭圆方程为
，知
，
，
设
，则
，
又，联立
，解得
，
6分
（2）显然不满足题意，所直线的斜率存在，可设的方程为，
设
，联立
， 8分
且△
10分
又为锐角，，
，
，
又
，
， 
12分
考点：直线与圆锥曲线的综合问题、设而不求思想.
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
