题目内容
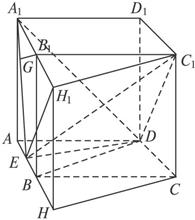
已知直平行六面体ABCD-A1B1C1D1的各条棱长均为3，∠BAD=60°．长为2的线段MN的一个端点M在DD1上运动，另一个端点N在底面ABCD上运动，则线段MN的中点P的轨迹（曲面）与共一个顶点D的三个面所围成的几何体的体积为
______．
|MN|=2，则|DP|=1，则点P轨迹是以点D为球心，半径r=1的球，
则球的体积为V=
π•r3=
，
∵∠BAD=60°∴∠ADC=120°=
•360°，
只取半球的
，则V=
π•
•
=
.；
故答案为
．
则球的体积为V=
| 4 |
| 3 |
| 4π |
| 3 |
∵∠BAD=60°∴∠ADC=120°=
| 1 |
| 3 |
只取半球的
| 1 |
| 3 |
| 4 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2π |
| 9 |
故答案为
| 2π |
| 9 |
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
相关题目
