题目内容
(14分)已知定义在 上的函数
上的函数 满足:
满足:
 ,且对于任意实数
,且对于任意实数 ,总有
,总有 成立.
成立.
(1)求 的值,并证明函数
的值,并证明函数 为偶函数;
为偶函数;
(2)若数列 满足
满足 ,求证:数列
,求证:数列 为等比数列;
为等比数列;
(3)若对于任意非零实数 ,总有
,总有 .设有理数
.设有理数 满足
满足 ,判断
,判断 和
和 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
【答案】
(1)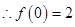 ,函数
,函数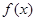 为偶函数
为偶函数
(2)略
(3)略
【解析】(1)令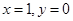 ,
,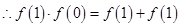 ,又
,又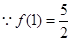 ,
,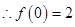 .…2分
.…2分
令 ,
,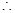
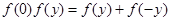 ,即
,即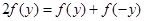 .
.
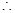
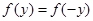 对任意的实数
对任意的实数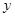 总成立,
总成立,
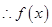 为偶函数.
4分
为偶函数.
4分
(2)令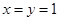 ,得
,得
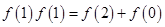 ,
,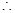
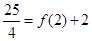 ,
,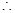
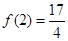 .
.
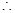
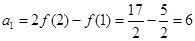 .…………………………………………………………5分
.…………………………………………………………5分
令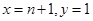 ,得
,得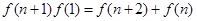 ,
,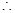
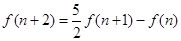 ………………………………………………………………6分
………………………………………………………………6分

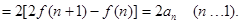 ………………………………………………8分
………………………………………………8分
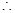
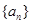 是以
是以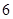 为首项,以
为首项,以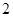 为公比的等比数列.
为公比的等比数列.
(3)结论: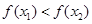 .………………………………………………………………9分
.………………………………………………………………9分
证明:设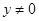 ,∵
,∵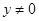 时,
时, ,
,
∴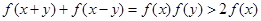 ,即
,即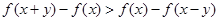 .……………………………………………………10分
.……………………………………………………10分
∴令 (
(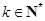 ),故
),故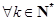 ,总有
,总有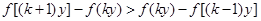 成立.
成立.
∴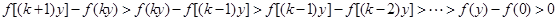 .………………………………………………………………………………………………11分
.………………………………………………………………………………………………11分
∴对于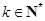 ,总有
,总有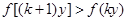 成立.
成立.
即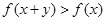
当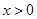 时,
时,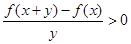
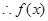 在
在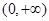 上单调递增。………………………………………………………………12分
上单调递增。………………………………………………………………12分
当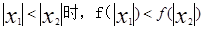 …………………………………………………………13分
…………………………………………………………13分
函数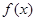 为偶函数,∴
为偶函数,∴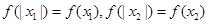 .∴
.∴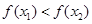 .……14分
.……14分

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目






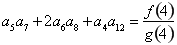

 上的函数
上的函数 满足
满足 ,当
,当 时,
时, ,若函数
,若函数 至少有6个零点,则
至少有6个零点,则 的取值范围是
( )
的取值范围是
( ) B.
B.
 D.
D.
 上的函数
上的函数 满足
满足 ,且
,且 ,
,
 ,若有穷数列
,若有穷数列 (
( )的前
)的前 项和等于
项和等于 ,则
,则 上的函数
上的函数 满足
满足 ,且
,且
 ,若有穷数列
,若有穷数列 (
( )的前
)的前 项和等于
项和等于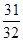 ,则
,则 上的函数
上的函数 满足
满足 ,且
,且 ,
,  ,若有穷数列
,若有穷数列 (
(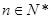 )的前
)的前 项和等于
项和等于 ,则n等于
,则n等于