题目内容
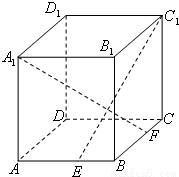
 16、如图:ABCD-A1B1C1D1是正方体.
16、如图:ABCD-A1B1C1D1是正方体.求证:(1)A1C⊥D1B1;
(2)A1C⊥BC1.
分析:(1)A1C1是线A1C在面A1B1C1D1内的射影,A1C1⊥B1D1,据三垂线定理可得A1C⊥B1D1 .
(2)的证明方法同(1),证明BC1和A1C在面BCC1B1的摄影B1C垂直,从而证明A1C⊥BC1.
(2)的证明方法同(1),证明BC1和A1C在面BCC1B1的摄影B1C垂直,从而证明A1C⊥BC1.
解答:解:(1)连A1C1,由正方体的性质得,A1C1⊥B1D1,
又CC1⊥面A1C1,A1C1是线A1C在面A1B1C1D1内的射影,由三垂线定理可知,A1C⊥B1D1 .
(2)连B1C,由正方体的性质得,BC1和B1C垂直,B1C是A1C在面BCC1B1内的摄影,
由三垂线定理可知,A1C⊥BC1.
又CC1⊥面A1C1,A1C1是线A1C在面A1B1C1D1内的射影,由三垂线定理可知,A1C⊥B1D1 .
(2)连B1C,由正方体的性质得,BC1和B1C垂直,B1C是A1C在面BCC1B1内的摄影,
由三垂线定理可知,A1C⊥BC1.
点评:先找出面的垂线,再找面的斜线,斜线在面内的射影可见,若此面内的一条直线和射影垂直,则此面内的该线就和此面的斜线垂直.

练习册系列答案
相关题目
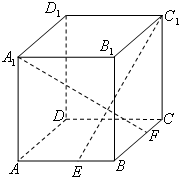 如图,ABCD-A1B1C1D1是棱长为6的正方体,E、F分别是棱AB、BC上的动点,且AE=BF.
如图,ABCD-A1B1C1D1是棱长为6的正方体,E、F分别是棱AB、BC上的动点,且AE=BF. 如图,ABCD-A1B1C1D1为正方体,下面结论中正确的是
如图,ABCD-A1B1C1D1为正方体,下面结论中正确的是 如图,ABCD-A1B1C1D1为正方体,下面结论中正确的结论是
如图,ABCD-A1B1C1D1为正方体,下面结论中正确的结论是