题目内容
函数 的值域为________.
的值域为________.
(-∞,0)
分析:根据分式函数的值域求法,得到真数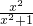 ∈(0,1),再结合底数为10的对数函数的单调性,可得原函数的值域.
∈(0,1),再结合底数为10的对数函数的单调性,可得原函数的值域.
解答:首先函数的定义域为{x|x≠0}
∵x2+1>1,可得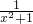 ∈(0,1),且
∈(0,1),且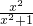 =1-
=1-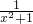 ,
,
∴0<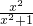 <1
<1
又∵10>1,函数y=lgx是增函数
∴ <lg1=0,可得函数
<lg1=0,可得函数 的值域为(-∞,0)
的值域为(-∞,0)
故答案为:(-∞,0)
点评:本题给出一个基本初等函数,叫我们求它的值域,着重考查了分式函数的值域求法和对数函数的单调性与值域等知识,属于基础题.
分析:根据分式函数的值域求法,得到真数
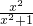 ∈(0,1),再结合底数为10的对数函数的单调性,可得原函数的值域.
∈(0,1),再结合底数为10的对数函数的单调性,可得原函数的值域.解答:首先函数的定义域为{x|x≠0}
∵x2+1>1,可得
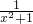 ∈(0,1),且
∈(0,1),且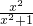 =1-
=1-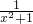 ,
,∴0<
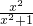 <1
<1又∵10>1,函数y=lgx是增函数
∴
 <lg1=0,可得函数
<lg1=0,可得函数 的值域为(-∞,0)
的值域为(-∞,0)故答案为:(-∞,0)
点评:本题给出一个基本初等函数,叫我们求它的值域,着重考查了分式函数的值域求法和对数函数的单调性与值域等知识,属于基础题.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 读图分析解答:设定义在闭区间[-4,4]上的函数y=f(x)的图象如图所示(图中坐标点都是实心点),完成以下几个问题:
读图分析解答:设定义在闭区间[-4,4]上的函数y=f(x)的图象如图所示(图中坐标点都是实心点),完成以下几个问题: