题目内容
已知平面向量 =(
=( ,1),
,1), =(
=( ),
), ,
, ,
, .
.
(1)当 时,求
时,求 的取值范围;
的取值范围;
(2)设 ,是否存在实数
,是否存在实数 ,使得
,使得 有最大值2,若存在,求出所有满足条件的
有最大值2,若存在,求出所有满足条件的 值,若不存在,说明理由
值,若不存在,说明理由
【答案】
(1)∵ =(
=( ,1),
,1), =(
=( )∴
)∴ ,
,

=
=
(1) 当 时,
时,

∵ ,∴
,∴
 时,
时, ,
, 时,
时,
∴ 的取值范围是
的取值范围是
(2)


① 当 ,即
,即 时,
时, ,由
,由 ,
,
得 (舍去)
(舍去)
② 当 ,即
,即 时,
时, ,
,
由 得
得 或
或 (舍去)
(舍去)
③当 >1,即
>1,即 >2时,
>2时, ,由
,由 ,
,
得 或
或 (舍去)
(舍去)
综上所述,存在 或
或 ,使得
,使得 有最大值
有最大值
【解析】(1)先根据向量的数量积及其坐标表示,确定y=f(x)的表达式,然后再根据式子特点结合函数的性质求值域.
(2)先确定函数g(x)的解析式,然后根据式子特点采用换元法转化为二次函数问题进行研究.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 =(
=( ,1),
,1), =(
=( ),
), ,
,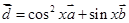 ,
, .(1)当
.(1)当 时,求
时,求 的取值范围;
的取值范围;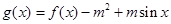 ,是否存在实数
,是否存在实数 ,使得
,使得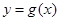 有最大值
有最大值 ,若存在,求出所有满足条件的
,若存在,求出所有满足条件的