Question

(本小题满分10分)已知集合A={x|x²-3x+2=0},B={x|x²-ax+3a-5=0}.若A∩B=B，求实数a的取值范围.

 

Answer 1

【答案】

当2≤a＜10时，均有A∩B=B.

【解析】主要考查集合的子集、交集运算。首先得出A={1,2},在由A∩B=B得出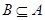，从而根据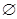B=及B≠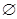两种情况，讨论x²-ax+3a-5=0根的判别式Δ＜0, Δ≥0时a的取值。

解:A={x|x²-3x+2=0}={1,2},

由x²-ax+3a-5=0，知Δ=a²-4(3a-5)=a²-12a+20=(a-2)(a-10).

(1)当2＜a＜10时，Δ＜0,B=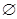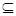A;

(2)当a≤2或a≥10时，Δ≥0，则B≠.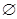

若x=1，则1-a+3a-5=0,得a=2,

此时B={x|x²-2x+1=0}={1}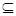A;

若x=2，则4-2a+3a-5=0，得a=1,

此时B={2,-1}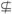A.

综上所述，当2≤a＜10时，均有A∩B=B.