题目内容
已知数列{an}是等差数列,a2=6,a5=18,数列{bn}的前n项和是Tn,且Tn+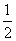 bn=1,
bn=1,
(1)求数列{an}的通项公式;
(2)求证数列{bn}是等比数列;
(3)记cn=an·bn,求证:cn+1≤cn。
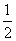 bn=1,
bn=1,(1)求数列{an}的通项公式;
(2)求证数列{bn}是等比数列;
(3)记cn=an·bn,求证:cn+1≤cn。
解:(1)由已知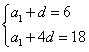 ,解得
,解得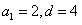 ,
,
∴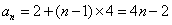 。
。
(2)由于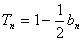 , ①
, ①
令n=1,得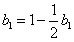 , 解得
, 解得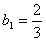 ,
,
当n≥2时,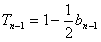 ,②
,②
①-②得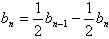 ,
,
∴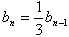 ,
,
又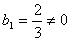 ,
,
∴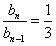 ,
,
∴数列{bn}是以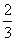 为首项,
为首项,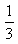 为公比的等比数列。
为公比的等比数列。
(3)由(2)可得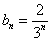 ,
,
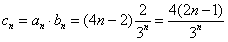 ,
,
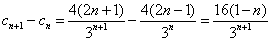 ,
,
∵n≥1,故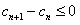 ,
,
∴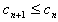 。
。
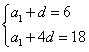 ,解得
,解得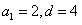 ,
, ∴
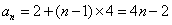 。
。(2)由于
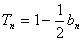 , ①
, ① 令n=1,得
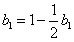 , 解得
, 解得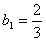 ,
,当n≥2时,
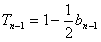 ,②
,② ①-②得
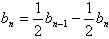 ,
, ∴
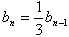 ,
,又
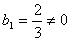 ,
,∴
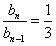 ,
,∴数列{bn}是以
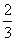 为首项,
为首项,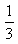 为公比的等比数列。
为公比的等比数列。(3)由(2)可得
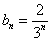 ,
,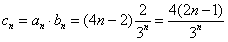 ,
,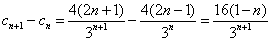 ,
, ∵n≥1,故
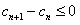 ,
,∴
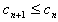 。
。
练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目