题目内容
已知数列 的前
的前 项和
项和 和通项
和通项 满足
满足 (
( ,
, 是大于0的常数,且
是大于0的常数,且 ),数列
),数列 是公比不为
是公比不为 的等比数列,
的等比数列, .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设 ,是否存在实数
,是否存在实数 ,使数列
,使数列 是等比数列?若存在,求出所有可能的实数
是等比数列?若存在,求出所有可能的实数 的值,若不存在说明理由;
的值,若不存在说明理由;
(Ⅲ)数列 是否能为等比数列?若能,请给出一个符合的条件的
是否能为等比数列?若能,请给出一个符合的条件的 和
和 的组合,若不能,请说明理由.
的组合,若不能,请说明理由.
解:(Ⅰ)当 时,
时,
 ,整理得
,整理得
又由 ,得
,得
结合q>0知,数列 是首项为q公比为
是首项为q公比为 的等比数列, ∴
的等比数列, ∴  分
分
(Ⅱ) 结合(Ⅰ)知,当q=2时, ,所以
,所以
假设存在实数 ,使数列
,使数列 是等比数列,则对任意n≥2有
是等比数列,则对任意n≥2有
(cn+1+λcn)2=(cn+2+λcn+1)(cn+λcn-1),将cn=2n+3n代入上式,得:
[2n+1+3n+1+λ(2n+3n)]2=[2n+2+3n+2+λ(2n+1+3n+1)]·[2n+3n+λ(2n-1+3n-1)],
即 [(2+λ)2n+(3+λ)3n]2=[(2+λ)2n+1+(3+λ)3n+1][(2+λ)2n-1+(3+λ)3n-1],
整理得 (2+λ)(3+λ)·2n·3n=0,解得λ=-2或λ=-3.
(2+λ)(3+λ)·2n·3n=0,解得λ=-2或λ=-3.
| 故存在实数实数 |

练习册系列答案
相关题目
 ,向前走了
,向前走了 米到达处测得塔顶的仰角为
米到达处测得塔顶的仰角为 ,则此塔的高度为__________米
,则此塔的高度为__________米
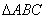 中,
中, 分别为角
分别为角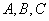 所对的边,且
所对的边,且 ,则角
,则角 =________.
=________. 满足
满足 则
则 .
. 的解集为
的解集为 .
. 的不等式
的不等式 的解集为
的解集为 ,若
,若 ,求实数
,求实数 的取值范围.
的取值范围.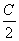 =0有一个根为1,则此三角形为( )
=0有一个根为1,则此三角形为( )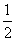 ,用Mn表示它的前n项之积,即Mn=a1·a2·a3…an,则数列{Mn}中的最大项是( )
,用Mn表示它的前n项之积,即Mn=a1·a2·a3…an,则数列{Mn}中的最大项是( ) 在
在 时的值时,
时的值时, 的值为( )
的值为( )  220 C. -57 D. 34
220 C. -57 D. 34 前
前 项和为
项和为 ,若
,若 ,
, ,则
,则 .
.