题目内容
已知函数 (a为常数).
(a为常数).(1)求f′(x);
(2)当a=1时,求f(x)在x∈
 上的最大值和最小值(e≈2.71828);
上的最大值和最小值(e≈2.71828);(3)求证:ln
 >
> .(n>1,且n∈N*)
.(n>1,且n∈N*)
【答案】分析:(1)直接利用导数的运算法则即可求出f′(x);
(2)把a=1代入其导函数,找到其在x∈ 上的单调性,即可求出其最大值和最小值;
上的单调性,即可求出其最大值和最小值;
(3)先由(2)知 在[1,+∞)上为增函数,再令
在[1,+∞)上为增函数,再令 ,利用x>1,f(x)>f(1)即可证明结论.
,利用x>1,f(x)>f(1)即可证明结论.
解答:解:(1)因为函数 ,
,
所以f'(x)=[ ]'+(lnx)'=
]'+(lnx)'=
即 .(2分)
.(2分)
(2)当a=1时, ,其中
,其中 ,
,
而 时,f'(x)<0;x∈(1,e]时,f'(x)>0,
时,f'(x)<0;x∈(1,e]时,f'(x)>0,
∴x=1是f(x)在 上唯一的极小值点,(4分)
上唯一的极小值点,(4分)
∴[f(x)]min=f(1)=0.(5分)
又 ,(6分)
,(6分)
∴ ,∴
,∴ .(7分)
.(7分)
综上,当a=1时,f(x)在 上的最大值和最小值分别为e-2和0.(8分)
上的最大值和最小值分别为e-2和0.(8分)
(3)若a=1时,由(2)知 在[1,+∞)上为增函数,(10分)
在[1,+∞)上为增函数,(10分)
当n>1时,令 ,则x>1,故f(x)>f(1)=0,(12分)
,则x>1,故f(x)>f(1)=0,(12分)
即 ,
,
∴ln >
> .(14分)
.(14分)
点评:本题主要考查利用导数求闭区间上函数的最值以及利用导数研究函数的单调性.利用导数研究函数的单调性,求解函数的单调区间、极值、最值问题,是函数和导数这一章最基本的知识,也是教学中的重点和难点.
(2)把a=1代入其导函数,找到其在x∈
 上的单调性,即可求出其最大值和最小值;
上的单调性,即可求出其最大值和最小值;(3)先由(2)知
 在[1,+∞)上为增函数,再令
在[1,+∞)上为增函数,再令 ,利用x>1,f(x)>f(1)即可证明结论.
,利用x>1,f(x)>f(1)即可证明结论.解答:解:(1)因为函数
 ,
,所以f'(x)=[
 ]'+(lnx)'=
]'+(lnx)'=
即
 .(2分)
.(2分)(2)当a=1时,
 ,其中
,其中 ,
,而
 时,f'(x)<0;x∈(1,e]时,f'(x)>0,
时,f'(x)<0;x∈(1,e]时,f'(x)>0,∴x=1是f(x)在
 上唯一的极小值点,(4分)
上唯一的极小值点,(4分)∴[f(x)]min=f(1)=0.(5分)
又
 ,(6分)
,(6分)∴
 ,∴
,∴ .(7分)
.(7分)综上,当a=1时,f(x)在
 上的最大值和最小值分别为e-2和0.(8分)
上的最大值和最小值分别为e-2和0.(8分)(3)若a=1时,由(2)知
 在[1,+∞)上为增函数,(10分)
在[1,+∞)上为增函数,(10分)当n>1时,令
 ,则x>1,故f(x)>f(1)=0,(12分)
,则x>1,故f(x)>f(1)=0,(12分)即
 ,
,∴ln
 >
> .(14分)
.(14分)点评:本题主要考查利用导数求闭区间上函数的最值以及利用导数研究函数的单调性.利用导数研究函数的单调性,求解函数的单调区间、极值、最值问题,是函数和导数这一章最基本的知识,也是教学中的重点和难点.

练习册系列答案
相关题目
 ( a为常数、a∈R),
( a为常数、a∈R), .
. (a为常数)的图象经过点(1,3).
(a为常数)的图象经过点(1,3). ( a为常数、a∈R),
( a为常数、a∈R), .
. (a为常数)是R上的奇函数,函数
(a为常数)是R上的奇函数,函数
 上恒成立,求t的取值范围
上恒成立,求t的取值范围 其中a为常数,且
其中a为常数,且 .
.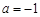 时,求
时,求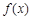 在
在 (e=2.718 28…)上的值域;
(e=2.718 28…)上的值域; 对任意
对任意 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.