题目内容
已知数列 的首项
的首项 ,且
,且 ,则
,则 为 ( )
为 ( )
| A.7 | B.15 | C.30 | D.31 |
D
解析试题分析:由 两边同加1,可得
两边同加1,可得 ,
, ,则
,则 是以2为首项,以2 为公比的等比数列.则
是以2为首项,以2 为公比的等比数列.则 ,所以
,所以 ,
, .
.
考点:构造法求数列的通项公式.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
等比数列 中,
中, ,
, ,则
,则 ( )
( )
A. | B. |
C. 或 或 | D. 或 或 |
等比数列 中,
中, ,
, ,则数列
,则数列 的公比为
的公比为
A. | B. | C. | D. |
等比数列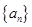 中,
中, ,则
,则 ( )
( )
A. | B. | C. | D. |
若等比数列 的前
的前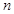 项和
项和 则
则 等于( )
等于( )
A. | B. | C.-1 | D.1 |
在等比数列{an}中,a1+an=34,a2an-1=64,且前n项和Sn=62,则项数n等于( )
| A.4 | B.5 | C.6 | D.7 |
已知数列{an}满足3an+1+an=0,a2= ,则{an}的前10项和等于( )
,则{an}的前10项和等于( )
A. |
B. |
C. |
D. |
公比为2的等比数列 的各项都是正数,且
的各项都是正数,且 则
则 = ( )
= ( )
| A.4 | B.-4 | C.2 | D.-2 |
已知等比数列{an}中,a2=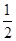 ,a3=
,a3= ,ak=
,ak= ,则k等于( )
,则k等于( )
| A.5 | B.6 | C.7 | D.8 |