题目内容
解不等式：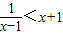
．
【答案】分析：将原不等式移项可得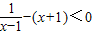
，通分后可化为
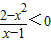，分解后可根据实数的性质转化为整式不等式
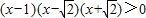，进而根据标根法（穿针引线法）得到不等式的解集．
解答：解：不等式：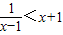
可化为
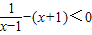
即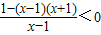
即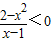
即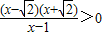
即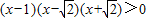
解得：-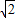
＜x＜1或x＞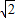
故原不等式的解集为（-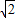
，1）∪（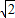
，+∞）
点评：本题考查的知识点是分式不等式的解法，解分式不等式，就是根据实数的性质，将其转化为整式不等式．
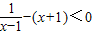，通分后可化为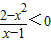，分解后可根据实数的性质转化为整式不等式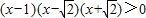，进而根据标根法（穿针引线法）得到不等式的解集．解答：解：不等式：
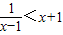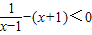
可化为即
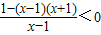
即
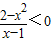
即
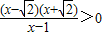
即
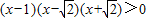
解得：-
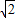＜x＜1或x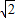＞故原不等式的解集为（-
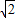，1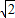）∪（，+∞）点评：本题考查的知识点是分式不等式的解法，解分式不等式，就是根据实数的性质，将其转化为整式不等式．
练习册系列答案
相关题目