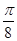题目内容
如图,单摆从某点开始来回摆动,离开平衡位置O的距离Scm和时间ts的函数关系式为S=6sin(2πt+ ),那么单摆来回摆动一次所需的时间为( )
),那么单摆来回摆动一次所需的时间为( )
| A.2πs | B.πs | C.0.5s | D.1s |
D
解析

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
 ( )
( )
A. | B. | C. | D. |
已知函数y=Asin(ωx+φ)+m的最大值为4,最小值为0.两个对称轴间最短距离为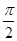 ,直线x=
,直线x= 是其图象的一条对称轴,则符合条件的解析式为( )
是其图象的一条对称轴,则符合条件的解析式为( )
A.y=4sin  | B.y=-2sin  +2 +2 |
C.y=-2sin  | D.y=2sin  +2 +2 |
设函数y=Asin(ωx+φ)(A>0,ω>0)在x= 时,取最大值A,在x=
时,取最大值A,在x= 时,取最小值-A,则当x=π时,函数y的值( )
时,取最小值-A,则当x=π时,函数y的值( )
| A.仅与ω有关 | B.仅与φ有关 |
| C.等于零 | D.与φ,ω均有关 |
设sin( +θ)=
+θ)= ,则sin2θ等于( )
,则sin2θ等于( )
A.- | B. | C. | D. |
函数y=- cos2x+
cos2x+ 的递增区间是( )
的递增区间是( )
A.(kπ,kπ+ )(k∈Z) )(k∈Z) |
B.(kπ+ ,kπ+π)(k∈Z) ,kπ+π)(k∈Z) |
| C.(2kπ,2kπ+π)(k∈Z) |
| D.(2kπ+π,2kπ+2π)(k∈Z) |
函数y=4sin(2x+ )的一个单调区间是 ( )
)的一个单调区间是 ( )
A.[ , , ] ] | B.[- , , ] ] |
C.[0, ] ] | D.[0, ] ] |
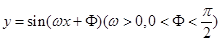 一个周期内的图象上的四个点,如图所示,
一个周期内的图象上的四个点,如图所示, B为
B为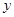 轴上的点,C为图像上的最低点,E为该函数图像的一个对称中心,B与D关于点E对称,
轴上的点,C为图像上的最低点,E为该函数图像的一个对称中心,B与D关于点E对称, 在
在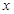 轴上的投影为
轴上的投影为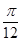 ,则
,则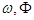 的值为( )
的值为( )
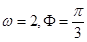 B.
B.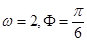
 D.
D.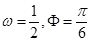
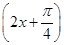 的图象向右平移φ(φ>0)个单位,再将图象上每一点横坐标缩短到原来的
的图象向右平移φ(φ>0)个单位,再将图象上每一点横坐标缩短到原来的 倍,所得图象关于直线x=
倍,所得图象关于直线x=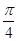 对称.则φ的最小正值为( )
对称.则φ的最小正值为( )