题目内容
f（x）是定义在（0，+∞）上的非负可导函数，且满足xf′（x）+f（x）≤0，对任意正数a、b，若a＜b，则必有（ ）A．af（b）≤bf（a）
B．bf（a）≤af（b）
C．af（a）≤f（b）
D．bf（b）≤f（a）
【答案】分析：先构造函数，再由导数与原函数的单调性的关系解决．
解答：解：xf′（x）+f（x）≤0⇒[xf（x）]′≤0⇒函数F（x）=xf（x）在（0，+∞）上为常函数或递减，
又0＜a＜b且f（x）非负，于是有：af（a）≥bf（b）≥0①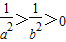
②
①②两式相乘得：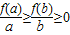
⇒af（b）≤bf（a），故选A．
点评：本题的难点在对不等式②的设计，需要经验更需要灵感．
解答：解：xf′（x）+f（x）≤0⇒[xf（x）]′≤0⇒函数F（x）=xf（x）在（0，+∞）上为常函数或递减，
又0＜a＜b且f（x）非负，于是有：af（a）≥bf（b）≥0①
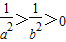②①②两式相乘得：
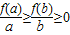⇒af（b）≤bf（a），故选A．点评：本题的难点在对不等式②的设计，需要经验更需要灵感．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
相关题目