题目内容
下列式子中(其中的 为平面向量),正确的是( )
为平面向量),正确的是( )A.

B.

C.

D.

【答案】分析:利用向量的三角形法则判断出A错;根据向量的数量积不满足结合律,数与向量的积满足结合律判断出B错C对;根据0与向量的积为零向量判断出D错.
解答:解:对于A,因为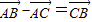 ,所以A错;
,所以A错;
对于B,因为向量的数量积不满足结合律,所以 ,所以B不对;
,所以B不对;
对于C,数与向量的积满足交换律,所以有 ,所以C对;
,所以C对;
对于D, 所以D错;
所以D错;
故选C
点评:本题考查两个向量的加减法的法则,以及其几何意义,两个向量的数量积的定义,理解两个向量运算的几何意义,是解题的关键.
解答:解:对于A,因为
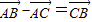 ,所以A错;
,所以A错;对于B,因为向量的数量积不满足结合律,所以
 ,所以B不对;
,所以B不对;对于C,数与向量的积满足交换律,所以有
 ,所以C对;
,所以C对;对于D,
 所以D错;
所以D错;故选C
点评:本题考查两个向量的加减法的法则,以及其几何意义,两个向量的数量积的定义,理解两个向量运算的几何意义,是解题的关键.

练习册系列答案
相关题目
下列式子中(其中的
,
,
为平面向量),正确的是( )
| a |
| b |
| c |
A、
| ||||||||||||
B、(
| ||||||||||||
C、λ(μ
| ||||||||||||
D、0•
|
 为平面向量),正确的是
为平面向量),正确的是


