题目内容
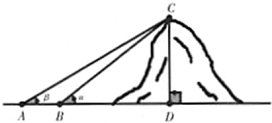如图所示，勘探队员朝一座山行进，在前后两处观察山顶的仰角分别是α，β，两个观察点之间的距离是d米．（I）若α=45°，β=30°，求sin（α-β）的值；
（II）求此山的高度CD．
分析：（I）利用差角的正弦公式，可求sin（α-β）的值；
（II）在△ABC中，由正弦定理求得BC，在直角△BCD中，由sinα=
可得CD=BCsinα．
（II）在△ABC中，由正弦定理求得BC，在直角△BCD中，由sinα=
| CD |
| BC |
解答：解：（I）若α=45°，β=30°，则sin（α-β）=sin（45°-30°）=sin45°cos30°-cos45°sin30°=
；
（II）∵∠ACB=α-β
∴在△ABC中，由正弦定理得
=
∴BC=
在直角△BCD中，由sinα=
可得CD=BCsinα=
即此山的高度是
| ||||
| 4 |
（II）∵∠ACB=α-β
∴在△ABC中，由正弦定理得
| d |
| sin(α-β) |
| BC |
| sinβ |
∴BC=
| dsinβ |
| sin(α-β) |
在直角△BCD中，由sinα=
| CD |
| BC |
| dsinαsinβ |
| sin(α-β) |
即此山的高度是
| dsinαsinβ |
| sin(α-β) |
点评：本题考查差角的正弦公式，考查正弦定理的运用，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
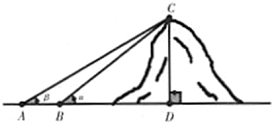如图所示，勘探队员朝一座山行进，在前后两处观察山顶的仰角分别是α，β，两个观察点之间的距离是d米．