题目内容
（本小题满分12分）
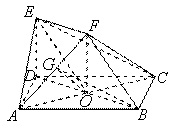
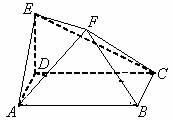如图，ABCD是边长为2的正方形，ED⊥平面ABCD，ED＝1，EF∥BD且EF＝
BD
(Ⅰ)求证：BF∥平面ACE；
(Ⅱ)求证：平面EAC
平面BDEF;
（Ⅲ）求二面角B－AF－C的大小．
|
面ACE，
面ACE，故BF∥平面ACE； …………………………4分 （2）因ED⊥平面ABCD，得ED⊥AC,又ABCD是正方形，
所以BD⊥AC，从而AC
平面BDEF，又AC
面ACE,
故平面EAC平面BDEF; ………………………8分
（3）过点O作OG⊥AF于点G，连接GB，则可证∠OGB为二面角B-AF-C的平面角．在Rt△FOA中，可求得OG=
，又OB=
，故
，∴
，即二面角B-AF-C的大小为
；…………………………12分
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
