题目内容
已知定义域为R的函数![]() 是奇函数。
是奇函数。
①求m、n的值。
②若对任意的t∈R,不等式![]() 恒成立,求实数k的取值范围。
恒成立,求实数k的取值范围。
解:①因为![]() 是奇函数,所以f (0)=0
是奇函数,所以f (0)=0
即![]()
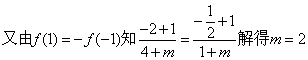
②由①知![]()
由上式知![]() 在(-∞,+∞)上为减函数。
在(-∞,+∞)上为减函数。
又因![]() 是奇函数,从而不等式
是奇函数,从而不等式![]() 等价于
等价于![]() ,因为
,因为![]() 是减函数
是减函数
由上式推得![]()
从而判别式![]() 。
。

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
题目内容
已知定义域为R的函数![]() 是奇函数。
是奇函数。
①求m、n的值。
②若对任意的t∈R,不等式![]() 恒成立,求实数k的取值范围。
恒成立,求实数k的取值范围。
解:①因为![]() 是奇函数,所以f (0)=0
是奇函数,所以f (0)=0
即![]()
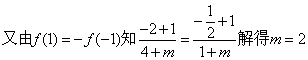
②由①知![]()
由上式知![]() 在(-∞,+∞)上为减函数。
在(-∞,+∞)上为减函数。
又因![]() 是奇函数,从而不等式
是奇函数,从而不等式![]() 等价于
等价于![]() ,因为
,因为![]() 是减函数
是减函数
由上式推得![]()
从而判别式![]() 。
。

 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案