题目内容
 如图,椭圆C:
如图,椭圆C:| x2 |
| 8 |
| y2 |
| 4 |
(Ⅰ)当△ABM的面积最大时,求直线AB的方程.
(Ⅱ)(ⅰ)试用θ表示|AF|;
(ⅱ)若|BF|=2|AF|,求直线AB的方程.
分析:(I)设AB的方程为x=my+2,A(x1,y1),B(x2,y2).将x=my+2代入椭圆方程可得根与系数的关系,可得|y1-y2|=
,由于S△ABM=
|FM| |y1-y2|=|y1-y2|,利用基本不等式即可得出此时的m,进而得到直线AB的方程.
(II)(i)由(I)可得椭圆的右焦点F(2,0),离心率e=
=
.右准线l:x=4.作AA1⊥l于点A1,则
=e=
,可得|AF|=
|AA1|=
(|FM|-|AF|cosθ)=
-
|AF|cosθ,即可得出|AF|.
(ii)同理|BF|=
,由|BF|=2|AF|,即可解得cosθ即tanθ,及直线的方程.
| (y1+y2)2-4y1y2 |
| 1 |
| 2 |
(II)(i)由(I)可得椭圆的右焦点F(2,0),离心率e=
| c |
| a |
| ||
| 2 |
| |AF| |
| |AA1| |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
(ii)同理|BF|=
| 2 | ||
|
解答:解:(I)设AB的方程为x=my+2,A(x1,y1),B(x2,y2).
将x=my+2代入
+
=1,消去x整理得(2+m2)y2+4my-4=0,△>0.
∴y1+y2=
,y1y2=
.
∴|y1-y2|=
=
=
,
∴S△ABM=
|FM| |y1-y2|=|y1-y2|=
≤
=2
,当且仅当m=0时取等号,此时直线AB的方程为x=2.
(II)(i)由(I)可得椭圆的右焦点F(2,0),离心率e=
=
.右准线l:x=4.
作AA1⊥l于点A1,则
=e=
,
∴|AF|=
|AA1|=
(|FM|-|AF|cosθ)=
-
|AF|cosθ,
∴|AF|=
.
(ii)同理|BF|=
,
由|BF|=2|AF|,得到
=2×
,解得cosθ=
,tanθ=
.
∴直线AB的方程为:y=
(x-2),化为
x-3y-2
=0.
将x=my+2代入
| x2 |
| 8 |
| y2 |
| 4 |
∴y1+y2=
| -4m |
| 2+m2 |
| -4 |
| 2+m2 |
∴|y1-y2|=
| (y1+y2)2-4y1y2 |
(
|
4
| ||
| 2+m2 |
∴S△ABM=
| 1 |
| 2 |
4
| ||||||
|
4
| ||
| 2 |
| 2 |
(II)(i)由(I)可得椭圆的右焦点F(2,0),离心率e=
| c |
| a |
| ||
| 2 |
作AA1⊥l于点A1,则
| |AF| |
| |AA1| |
| ||
| 2 |
∴|AF|=
| ||
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
∴|AF|=
| 2 | ||
|
(ii)同理|BF|=
| 2 | ||
|
由|BF|=2|AF|,得到
| 2 | ||
|
| 2 | ||
|
| ||
| 3 |
| ||
| 3 |
∴直线AB的方程为:y=
| ||
| 3 |
| 7 |
| 7 |
点评:本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立得到根与系数的关系、三角形的面积计算公式、椭圆的第二定义、直线的方程等基础知识与基本技能方法,属于难题.

练习册系列答案
相关题目
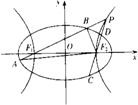 如图,已知椭圆
如图,已知椭圆 如图所示,A、B是椭圆的两个顶点,C是线段AB的中点,F为椭圆的右焦点,射线OC交椭圆于点M,且|OF|=2,若MF⊥OA,则此椭圆的标准方程为
如图所示,A、B是椭圆的两个顶点,C是线段AB的中点,F为椭圆的右焦点,射线OC交椭圆于点M,且|OF|=2,若MF⊥OA,则此椭圆的标准方程为