题目内容
设数列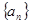 的首项
的首项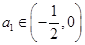 ,
,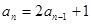
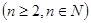
⑴求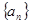 的通项公式(
的通项公式(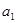 已知)
已知)
⑵设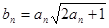 ,证明:
,证明: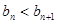
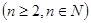 。
。
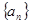 的首项
的首项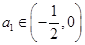 ,
,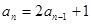
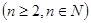
⑴求
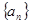 的通项公式(
的通项公式(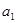 已知)
已知)⑵设
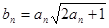 ,证明:
,证明: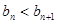
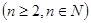 。
。(1) ;(2)见解析.
;(2)见解析.
 ;(2)见解析.
;(2)见解析.构造法,先求等比数列的通项公式;利用递推关系证明不等式。
解:(1)

 (需验证
(需验证 的情形)…………=……….6分
的情形)…………=……….6分
(2)因为

因为 ,代入之后可以证明。…………=……….12分
,代入之后可以证明。…………=……….12分
解:(1)

 (需验证
(需验证 的情形)…………=……….6分
的情形)…………=……….6分(2)因为

因为
 ,代入之后可以证明。…………=……….12分
,代入之后可以证明。…………=……….12分
练习册系列答案
相关题目
 中,
中, 、
、 ,则
,则 =( )
=( ) 若存在两项
若存在两项 、
、 使得
使得 ,且有
,且有 ≥
≥ 对上述
对上述 恒成立,求x的取值范围.
恒成立,求x的取值范围. 的前n项和中,
的前n项和中, 最小,且
最小,且 ,前n项和
,前n项和 ,求n和公比q
,求n和公比q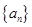 ,定义
,定义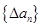 为数列
为数列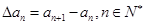 ;对
;对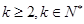 ,定义
,定义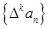 为
为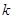 阶差分数列,其中
阶差分数列,其中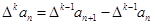 .
.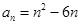 ,分别求出其一阶差分数列
,分别求出其一阶差分数列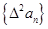 的通项公式;
的通项公式;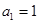 ,且满足
,且满足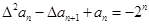 ,求出数列
,求出数列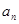 及前
及前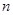 项和
项和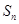 .
. ”是“a,b,c成等比数列”的( )
”是“a,b,c成等比数列”的( ) 是等比数列,
是等比数列, ,则
,则 ( )
( )



 是等比数列{
是等比数列{ }的前n项和.且 S
}的前n项和.且 S =1,S
=1,S =3,则S
=3,则S =
=  的公比为正数,且
的公比为正数,且 ,
, ,则
,则



