题目内容
正四棱锥P-ABCD的五个顶点在同一个球面上，若其底面边长为4，侧棱长为
，则此球的表面积为
- A.18π
- B.36π
- C.72π
- D.9π
B
分析：先利用勾股定理求出正四棱锥的高PM，再用射影定理求出球的半径，代入面积公式计算求得表面积．
解答：设球的半径为r，正方形的ABCD的对角线的交点 M，则球心在直线PM上．
MC=
AC=2
，
由勾股定理得 PM=
=
=4，
再由射影定理得 PC2=PM×2r，
即 24=4×2r，∴r=3，∴此球的表面积为 4πr2=36π，
故选B．
点评：本题考查勾股定理、射影定理的应用以及求得表面积公式．
分析：先利用勾股定理求出正四棱锥的高PM，再用射影定理求出球的半径，代入面积公式计算求得表面积．
解答：设球的半径为r，正方形的ABCD的对角线的交点 M，则球心在直线PM上．
MC=
AC=2，由勾股定理得 PM=
==4，再由射影定理得 PC2=PM×2r，
即 24=4×2r，∴r=3，∴此球的表面积为 4πr2=36π，
故选B．
点评：本题考查勾股定理、射影定理的应用以及求得表面积公式．
练习册系列答案
相关题目
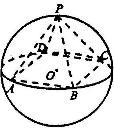如图，正四棱锥P-ABCD底面的四个顶点A、B、C、D在球O的同一个大圆上，点P在球面上，如果VP-ABCD=| 16 |
| 3 |
| A、4π | B、8π |
| C、12π | D、16π |
（2009•温州一模）如图是正四棱锥P-ABCD的三视图，其中正视图是边长为1的正三角形，则这个四棱锥的表面积是（ ）