题目内容
若函数f(x) =sin2ax-sinaxcosax(a>0) 的图象与直线y=m相切,相邻切点之间的距离为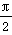
(1)求m和a的值;
(2)若点A(x0,y0)是y=f(x)图象的对称中心,且x0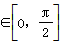 ,求点A的坐标
,求点A的坐标
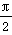
(1)求m和a的值;
(2)若点A(x0,y0)是y=f(x)图象的对称中心,且x0
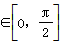 ,求点A的坐标
,求点A的坐标 解:(1)f(x)=sin2ax-sinaxcosax=-sin2ax=-sin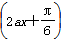 +
+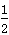 ,
,
由题意知,m为f(x) 的最大值或最小值,
所以m=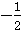 或m=
或m=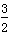 ;
;
由题设知,函数f(x) 的周期为, a=2 ,
a=2 ,
所以m=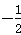 或m=
或m=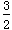 ,a=2.
,a=2.
(2)∵f(x)=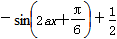 ,
,
 令sin=0,得4x+
令sin=0,得4x+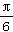 =k
=k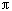 (k
(k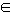 Z),
Z),
 x=
x=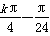 (k
(k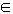 Z),
Z),
由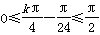 (k
(k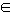 Z),得k=1或k=2,
Z),得k=1或k=2,
因此点A的坐标为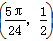 或
或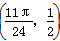 .
.
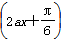 +
+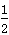 ,
, 由题意知,m为f(x) 的最大值或最小值,
所以m=
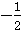 或m=
或m=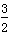 ;
; 由题设知,函数f(x) 的周期为,
 a=2 ,
a=2 ,所以m=
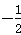 或m=
或m=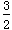 ,a=2.
,a=2. (2)∵f(x)=
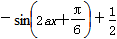 ,
, 令sin=0,得4x+
令sin=0,得4x+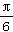 =k
=k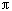 (k
(k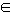 Z),
Z), x=
x=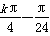 (k
(k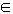 Z),
Z), 由
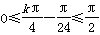 (k
(k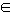 Z),得k=1或k=2,
Z),得k=1或k=2,因此点A的坐标为
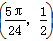 或
或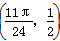 .
. 
练习册系列答案
相关题目